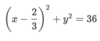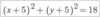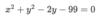Geometry (Problems 1.) Flashcards
Find the “x” value in the triangle below.
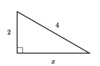
x = 2√3
Find the x value in the triangle below.
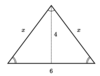
x = 5
Create a Proof for the 45°-45°-90° Triangle Equation
- Establish that a 45°-45°-90° Triangle has two equal length sides.
- From that information we can Establish that in the Pythagorean Theorem, A = B, and we can Substitute one with the other.
- Simplify the equation and solve for A or B to determine that
A = B = (√2/2) C
or
(√2) A = (√2) B = C
Find the length of the unknown sides in the triangle shown below
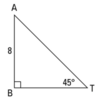
hypotenuse = 8√2
Leg = 8
Create a proof for the sides of a 30° 60° 90° Triangle.
- Create an Equilateral Triangle and label all the sides and angles.
- Split the Equilateral Triangle down the middle and label the new sides and angles.
- Create an equation using the Pythagorean Theorem to find the missing side.
- Solve and Simplify the equation for the missing side “a.”
Solve for the missing side of the Triangle.
6√3
What is the Sin, Cos, and Tan of angle “F.”
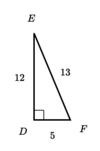
Sin (F) = 12/13
Cos (F) = 5/13
Tan (F) = 12/5
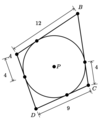
Find the missing sides of the triangle
Round your answer to the nearest hundredth.
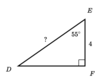
x = 6.97
y = 5.71
Find the missing angle of the triangle
Round your answer to the nearest hundredth.
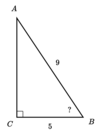
56.25°
Find the missing angle “B”.
angle “B” = 53.68°
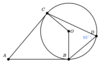
Find the missing side “AB”
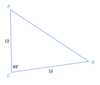
side “AB” = 18.03
Find the missing angles
angle “A” = 48.37°
angle “B” = 76.33°
angle “C” = 55.30°
Find the missing side “BC”
side “BC” = 8.8
What is the Arc Measure, in degrees, of arc (AC) on circle P below?
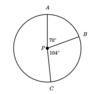
174°
In the figure below, line (DB) and (AC) are diameters of circle P. The length of line (PB) is 8 units.
What is the length of curve (DC)?
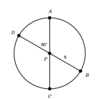
(16/3)π
or
16.76
In the figure below, the radius of circle p is 10 units. Arc (ABC) has a length of 16π.
What is the measure of Arc (AC), in degrees?
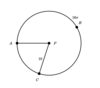
72°
Convert the angle Ø = (8π/9) radians to degrees.
160°
Convert the angle Ø = 290° to radians.
29π/18 Radians
What is the exact length of Curve (BCA)?
85π/2
What is the arc measure of Curve (AB), in radians?
17π/30
What is the area of the Sector?
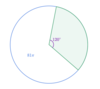
27π
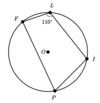
If angle “ADC” measures 23º, what does angle “ABC” measure?
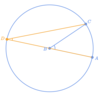
angle “ABC” = 46°
Create a Proof that Triangles created by angles subtending a circles diameter are Right Triangles.
- Create an image of a random triangle subtending a circles diameter.
- Cut the triangle in half and label the sides as “r”
- Realize that the central angle is twice as long as the other angle subtending the same arc and label the angles.
- Create an equation for the central triangle to determine the other two angles.
- Once solved, add the theata to the other angle to create a 90° angle
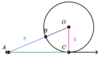
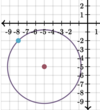
What is the Radius of circle “O”
Radius = 8.5 Units
The measure of Curve “LI” is 97°, what is the measure of Curve “FL”.
Curve “FL” = 43°
What is the length of Line “AC”
Line “AC” = 12 Units
What is the measure of Angle “A” ?
Angle “A” = 50°
What is the perimeter of Quadrilateral “ABCD” ?
Quadrilateral “ABCD” = 42 Units
The equation of a Circle is given below
What is the Center and Radius?
Center = (2/3 , 0)
Radius = 6 Units
Write and equation for the circle below
The equation of a Circle is given below
What is the Center and Radius?
Center = (0 , 1)
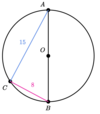
Radius = 10 Units
