Geometry (Equations) Flashcards
Pythagorean Theorem
a2 + b2 = c2
- In a Right Triangle, the area of the square whose side is the “hypotenuse” is equal to the sum of the areas of the squares of the other two sides.
45°-45°-90° Triangle Equation for the Hypotenuse
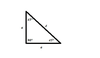
A = B = (√2/2) C
or
(√2) A = (√2) B = C
Destinguishing a 45° 45° 90° Triangle
- The two sides that aren’t the hyptotenuse will be the same length
- When given the hypotenuse, the other side of the triangle will be half the length of the Hypotenuse multiplied by √2.
- To find the hypotenuse just multiply the a leg of the Triangle by √2.
30° 60° 90° Triangle Equation for the hypotenuse
- The side opposite the 90° angle is equal to “x.”
- The side opposite the 30° angle is 1(x)/2.
- The side opposite the 60° angle is √3(x)/2.
Destinguishing a 30° 60° 90 °Triangle
The Hypotenuse will either be (The length of the shortest side multiplied by 2) or (The length of the second longest side divided by √3 then multiplied by two).
The second longest side (opposite the 60° angle) will either be (The length of the shortest side multiplied by √3) or (The length of the hypotenuse divided by two, then multiplied by √3).
The shortest length (opposite the 30° angle) will either be (The length of the hypotenuse divided by 2) or (The length of the second longest side divided by √3).
Area of a Triangle Equation
Multiply the base of the Triangle by the height, then divide by 2.
Law of Sines Equation
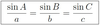
Law of Cosines Equation
* The side opposite the given angle is
(The missing side squared =
side b (squared) + side c (squared) - 2(bc)cos(σ)
Radius (From Diameter)
Equation
r = d/2
Diameter (From Radius)
Equation
d = 2r
π (From Circumference and Diameter)
(Equation)
π = c/d
π (From Circumference and Radius)
(Equation)
π = c/2r
Circumference (From Diameter and π)
(Equation)
c = dπ
Circumference (From Radius and π)
(Equation)
c = 2πr
Diameter (From π and Circumference)
(Equation)
d = c/π
