Geometry Ch. 6 Flashcards
(16 cards)
line of symmetry
a line of symmmetry is the imaginary line where you could fold the image and have both halves match exactly
Theorem 16: How can you determine a perpendicular bisector?
in a plane, two points each equidistant from the endpoints of a line determine the perpendicular bisector of a line segment

transversal
a line that passes through two other lines
Theorem 17: What can you say about corresponding angles of parallel lines?
Corresponding angles of parallel lines are equal.
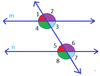
Corallary 1 of Theorem 17: How do alternate interior angles relate to each other in parallel lines?
Alternate interior angles of parallel lines are equal.

Corallary 2 of Theorem 17: How do interior angles on the same side of the transversal of parallel lines relate to each other?
interior angles of on the same side of the transversal of parallel lines are supplementary
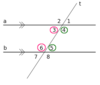
Corallary 3 of Theorem 17: What can you say about two lines perpendicular to a third line?
In a plane, two lines that are perpendicular to a third line are parallel to eachother

Postulate 7: How many lines can be drawn through a point not on a parallel line to create a parallel line?
Through a point not on a line, there is exactly one line parallel to the given line

Theorem 18: What can you say about two lines parallel to a third line?
In a plane, two lines parallel to a third line are all parallel to each other.

Theorem 20: What can you say about the sum of the angles of a triangle?
The sum of all three angles of a triangle is 180°
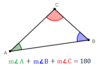
Corallary 1 to Theorem 20 : What can you say about a third angle if two angles of one triangle are equal to two angles of a second triangle?
If two angles of one triangle are equal to two angles of another triangle, then the third angles of both triangles are equal
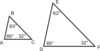
Corallary 2 to Theorem 20: What can you say about the acute angles of a right triangle?
The acute angles of a right triangle are complementary (they add to 90°).
Corallary 3 to Theorem 20: What is the angle measurement of one angle in an equilateral triangle?
Each angle of an equilateral triangle is 60°.

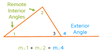
Theorem 21: What is the exterior angle of a triangle equal to?
The exterior angle of a triangle is equal to the sum of the remote interior angles.
Theorem 22: AAS (not ASS which is not congruent!)
If two angles and the side opposite them of one triangle are equal to the corresponding parts of another triangle, then the triangles are congruent.

Theorem 23: HL (The only time ASS works!)
If the hypoteneuse and leg of one right triangle are equal to the corresponding parts of another right triangle, then the triangles are congruent.