Geometry Ch. 11

Question 1

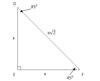
Theorem 50: Isosceles Right Triangle

Answer 1

c = x√2 (the hypoteneus of an isosceles right triangle is √2 times the side length)

Question 2

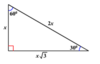
Theorem 51: 30°-60°- 90° Triangle

Answer 2

in a 30-60-90 Triangle, if the small leg is x, then c=2x and b=x√3

Question 3

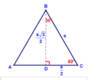
Corollary to Theorem 51: Altitude of an Equilateral Triangle

Answer 3

h = s/2 ∙ √3 the altitude of an equilateral triangle is √3 times one half the side length

Question 4

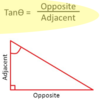
tangent ratio

Answer 4

tangent of an angle = opposite/ adjacent (TOA)

Question 5

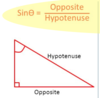
sine ratio

Answer 5

sine of an angle = opposite/ hypotenuse (SOH)

Question 6

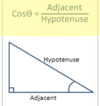
cosine ratio

Answer 6

cosine of an angle = adjacent/ hypotenuse (CAH)

Question 7

inverse tangent (tan⁻¹)

Answer 7

use inverse tangent when you know that ratio of the side lengths, but you don’t know the angle

tan ∠? = 1, do tan⁻¹ 1 = 45°

Question 8

slope

Answer 8

slope = rise/ run or (y₂-y₁)/ (x₂-x₁)

Question 9

angle of inclination

Answer 9

the angle created where the line intersects another horizontal line (often the x axis).

Use tan⁻¹ (slope) to find the angle of inclination

Question 10

Theorem 52: the slopes of parallel lines

Answer 10

Two nonvertical lines are parallel iff their slopes are equal

Question 11

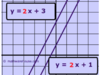
Theorem 53: the slopes of perpendicular lines

Answer 11

Two nonvertical lines are perpendicular iff their slopes are the negative reciprocal of each other.