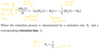Fundamentals of Magnetic Resonance Flashcards
(97 cards)
What is nuclear spin?
Nuclei have an intrinsic total angular momentum - the operator for nuclear spin is a bold captial I with a hat to show it is a vector and an operator
The nuclei spin quantum number (total angular momentum quantum no.) is I with units bof angular momentum per nucleus
Total angular momentum is measured in units of ħ (h/2π)
What is Planck’s constant?
a fundamental quantity that is equal to the energy per unit frequency of a quantum of electromagnetic radiation
E = hv = ħω
h = 6.626 x 10-34 J/Hz
ħ = h/2π
What values can nuclear spin take?
Can be an integar or half integar
When protons = even and neutrons = even and mass number is even the spin is 0
When protons = odd and neutrons = even and mass no = odd the spin is half integar
When protons = even and neutrons = odd and mass no. = odd the spin is half intear
When protons = odd, neutrons = odd and mass no. = even the spin is an integar value
What is total angular momentum?
A vector
I = {Ix, Iy, Iz}
What are the eigenvalues and eigenfunctions of Iz?
Izψm = mħψm
ψm - eienfunction
mħ - eigenvalue
m - quantum number for Iz
The number of values of m are 2I + 1
the values of m are {-I, -I+1 …… +I}
What is the nuclear magnetic momentum?
Nuclei with nuclear spin have a nuclear magnetic moment μ (with a hat)
μ = {μx, μy, μz) - vector operator
μ is proportional to anuglar momentum: μ = γI
γ is the constant of proportionality - gyromanetic ratio which is a property of the nucleus measured in rad s-1 T-1 (or MHzT-1 if it is γ/2π)
What is the Zeeman interaction?
The interaction between the nuclear magnetic moment and anyapplied magnetic field B0
The energy of this interaction is described by the Zeeman Hamiltonian Hz
- H*z = -μ x B = -γI x B = -γB0Iz
- H*z is the Zeeman Hamiltonian, μ is the magnetic moment, B is the field vector, I is the angular momentum, γ is the gyromanetic ratio, B0 is the applied magnetic field defined in the z direction, Iz is the z component of the angular momentum
How do we find the eigenvalues and eigenfunctions of the Zeeman Hamiltonian?
Solve the time-independent Schrodinger equation: Hzψ = Eψ
- γB0mħψ = Eψ
- γB0mħψm = Emψm
Eigenfunctions: ψm
Eigenvalues: Em = -γB0mħ

What is the difference in energy between the two spin states?
|ΔE| = | (-1/2γB0ħ) - (1/2γB0ħ) | = γB0ħ
What is the frequency of energy required to make a transition between ther spin states?
ΔE = γB0ħ
ΔE = ħω
.’. γB0ħ = ħω - cancel the ħ
γB0 = ω (rad s-1)
This is the Larmor frequency
ω is different for different nuclei in the same field
ω is the same for higher spin nuclei
What is the selection rule for NMR and why?
Δm = ±1
so that the Larmor frequency is the same for all values of I
The Larmor frequency of 1H is 42.577 (γ) x 9.4 (B0) = 400 MHz
Why do nuclei of the same type in different chemical environments have different Larmor frequencies (why does chemical shift change)?
The electron density around the nucleus generates a weak induced magnetic field at the nucleus
Bind = -σiB0
Bind is the induced field, σi is the isotropic shielding constant and B0 is proportional to the main field
The -ve sin means the induced field is in the opposite direction to the main field
What is the effective field felt by each nucleus?
The sum of the applied field, B0, and the induced field, Bind.
Beff = B0 + Bind = (1 - σi)B0
The larmor frequency is proportional to the local field at the nucleus - Beff
ω = γBeff = γ (1 - σ) B0 = (1 - σi) ω0 where ω0 is the shift in the larmor frequency
Why do we use ppm?
The isotropic chemical shift parameter σi is a chemical property but the Larmor frequency that is measured is an experimental property because it depends on the exact B0
ppm is a standard way to describe chemical shifts that is independant of the applied field
ppm is a relative scale - a fraction of the Larmor frequency
How do we define chemical shift in ppm?
For 1H and 13C chemical shift is defined in terms of TMS as δ = 0
All chemical shift is measured relative to a reference compound

How do you convert ppm to frequency in Hz?
Multiply the chemical shift by the reference frequency in MHz
relative frequency = chemical shift (ppm) x Larmor frequency (MHz)
(v - vref) = δ x vref (MHz)
How do you calculate the difference between two peaks in Hz?
Take the differencebetween peaks in ppm and multiply by the reference frequency
Δv = (δ1 - δ2) x vref (MHz)
What is the difference between an NMR experiment and an MRI test?
In a normal NMr experiment a very homogenous magnetic field is used to make sure all nuclei experience the same field and small differences in the Larmor frequency due to chemical shift can be detected
In MRIs we deliberately apply a magnetic field that varies as a function of position - magnetic field radient Gx and has units of T m-1
Btotal(x) = B0 + Gx
What do we obtain if a magnetic field gradient is used on an NMR experiment?
An image of the sample is obtained because the Larmor frequency is directly proportional to the position of each nucleus
ω(x) = γBtotal(x) = ω0 + γGxx
where ω is the Larmor frequency which depends on position and x is the position
What is the probability of a nucleus being in a spin state ψm?

How do we determine how many nuclei are in each spin state?
Using Boltzmann statistics
Nuclei populate both energy states almost equally
What is nuclear polarisation, P?
The difference in population between the spins states
What is the energy level picture for NMR?
useful way to think about frequencies in an NMR spectrum
Cannot think about NMR in terms of nuclei in the ground state being excited to a higher state then relaxing to ground state
Transition between the states are continuous even in equilibrium
There is a slightly higher probability for transition from -1/2 to 1/2 so a equilibrium there is a population imbalance with an excess of spins in the low energy state
Is NMR relaxation provide the NMR signal?
Relaxation estabilishes the population difference but does not gve rise to the NMR signal
Not enough absorption for detection- requires resonance amplification