forces Flashcards
When forces are applied to materials, the…. can change
the size and shape
draw apparatum hook’s law
and describe experiment
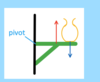
Set up the apparatus as shown in the diagram.
A single mass (0.1 kg, 100g) is attached to the spring, with a pointer attached to the bottom, and the position of the spring is measured against the ruler.
The mass (in kg) and position (in cm) are recorded in a table.
A further mass is added and the new position measured.
The above process continues until a total of 7 masses have been added.
The masses are then removed and the entire process repeated again, until it has been carried out a total of 3 times, and averages can then be taken.
Once measurements have been taken:
The force on the spring can be found by multiplying the mass on the spring (in kg) by 10 N/kg (the gravitational field strength).
The extension of the spring can be found by subtracting the original position of the spring from each of the subsequent positions.
Finally, a graph of extension (on the y-axis) against force (on the x-axis) should be plotted.
A graph of extension against force for a metal spring
Hooke’s law states that:
The extension of a spring is proportional to the applied force.
force hooke’s law equation
Hooke’s law is associated with the … of a force-extension graph.
initial linear (straight)
Objects that obey Hooke’s law will
return to their original length after being stretched.
If an object continues to be stretched it can be taken past the
at this point will no longer
limit of proportionality (sometimes called the elastic limit).
At this point the object will no longer obey Hooke’s law and will not return to its original length.
A relationship is said to be proportional if the graph is a
straight line going through the origin.
the relationship is linear if
a graph is a straight line but does not go through the origin
forces can
change the spped of an object
change the direction of movement of an object
change the shape of an object
change the size of an object
When several forces act on a body, the resultant (overall) force on the body can be found by
adding together forces which act in the same direction and subtracting forces which act in opposite directions:
When the forces acting on a body are balanced (i.e. there is no resultant force), the body will
ither remain at rest or continue to move in a straight line at a constant speed.
Friction is
a force that opposes the motion of an object caused by the contact (rubbing) of two surfaces. It always acts in the opposite direction to the direction in which the object is moving.
Air resistance (sometimes called drag) is a form of friction caused by
Friction (including air resistance) results in
a body moving through the air.
energy loss due to the transfer of energy from kinetic to internal (heat).
The resultant force is sometimes also known as the
net force or the unbalanced force.
Force, mass and acceleration are related by the following equation:
The greater the force, the the acceleration (for a given mass).
For a given force, the smaller the mass the the acceleration.
greater
greater
If you are trying to find the acceleration, check that you know both the
unbalanced (resultant) force and the mass of the object.
If you don’t, you might need to calculate the acceleration using a different equation.
A moment is the
turning effect of a force.
Diagram showing the moment of a force exerted by a spanner on a nut
The principle of moments states that
For a system to be balanced, the sum of clockwise moments must be equal to the sum of anticlockwise moments.
In the above diagram:
Force F2 is supplying a clockwise moment;
Forces F1 and F3 are supplying anticlockwise moments.
F2 × d2 = F1 × d1 + F3 × d3
Example of The Principle of Momen
To prevent the shelf from collapsing, the support must provide an upward moment equal to the downward moment of the vase
Demonstrating Equilibrium
A simple experiment to demonstrate that there is no net moment on an object in equilibrium involves taking an object, such as a beam, and replacing the supports with newton (force) meters:
The beam in the above diagram is in equilibrium.
The various forces acting on the beam can be found either by taking readings from the newton meters or by measuring the masses (and hence calculating the weights) of the beam and the mass suspended from the beam.
The distance of each force from the end of the ruler can then be measured, allowing the moment of each force about the end of the ruler to be calculated.
It can then be shown that the sum of clockwise moments (due to forces F2 and F3) equal the sum of anticlockwise moments (due to forces F1 and F4).
For a symmetrical object of uniform density (such as a symmetrical cardboard shape) the centre of mass is located at
the point of symmetry:
experiment finding centre of mass of irregular shapes
When an object is suspended from a point, the object will always settle so that its centre of mass comes to rest below the pivoting point.
This can be used to find the centre of mass of an irregular shape:
The irregular shape (a plane laminar) is suspended from a pivot and allowed to settle.
A plumb line (lead weight) is then held next to the pivot and and a pencil is used to draw a vertical line from the pivot (the centre of mass must be somewhere on this line).
The process is then repeated, suspending the shape from two different points.
The centre of mass is located at the point where all three lines cross.
An object is stable when
its centre of mass lies above its base.
Some other common scalars and vectors are given below:
vectors can be added together using the following rules
f two vectors point in the same direction, the resultant vector will also have the same directions and its value will be the result of adding the magnitudes of the two original vectors together.
If two vectors point in opposite directions then subtract the magnitude of one of the vectors from the other one. The direction of the resultant will be the same as the larger of the two original vectors
If the two vectors point in completely different directions, then the value of the resultant vector can be found graphically:
Draw an arrow representing the first vector.
Now starting at the head of the first arrow, draw a second arrow representing the second vector.
The resultant vector can be found by drawing an arrow going from the tail of the first vector to the tip of the second vector.
