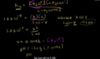EK Chem Ch7 Acid, Bases,Titration Flashcards
Titration
Titration is the process of finding / to determine the concentration of an unknown solution (the analyte) by reacting it with a solution of known concentration (the titrant). A solution of known concenteartion is used to determine the concentration of an unknown solution (titrand or analyte)
The analyte is generally placed in an Erlenmeyer flask, while the titrant is placed in a burette so that the volume of solution added can be monitored.
The titrant is added to the analyte until the endpoint is reached. Calculations are then performed to find the unknown concentration of the analyte. Titrations are typically performed for acid/base reactions but are not limited to them.
equivalence point titration
At equivalence points during the titration, the number of acid or base groups added to the solution is equivalent to the number of base/acid groups in the original unknown solution. We can calculate our unknown concentration or volume using the formula NaVa = NbVb, where N and V are the normality (mol/L) and volume of the acidic and basic solutions, respectively. It is important to convert from molarity (M) to normality (N) for polyprotic acids and polyvalent bases.
flat regions of titration curves
=represent buffering solutions (a roughly equal mix of an acid/base and its conjugate), while the steep, near-vertical sections of the curve contain equivalence point(s), which indicate that enough of the titrant has been added to completely remove one equivalent (acid or base group) from each of the original molecules in the unknown solution. Species with multiple acid or base groups (e.g. H3PO4 or Ca(OH)2) will have multiple equivalence points during the titration.
end point of titration
The final key point of any titration is the endpoint. To be successful, there must be some method for observing the endpoint of the reaction. The type of titration reaction that is being used will determine the method used for observing the endpoint. For example, in an acid-base titration, a specific pH value will be the endpoint (monitored by color-changing indicators), while for precipitation reactions, the endpoint is realized by the appearance of a precipitate. Regardless of the details of the reaction involved, the goal of titrations is always to use known volumes/concentrations to determine unknown volumes/concentrations.
Based on Figure 2, what is the approximate pKa of the carboxylic acid group in glycine?
answer is 2.4, In the Henderson-Hasselbalch equation, pH = pKa + log[B]/[A], where B is the conjugate base of the weak acid (represented by A). If [B] = [A], the pH will equal the pKa. This occurs for the first plateau in the titration curve for glycine shown in Figure 2. Estimating the pH at the middle of the first plateau gives a value closest to 2.4, as shown below.
Ka
Acidic species can be strong (for the exam, assume that strong acids completely dissociate in water) or weak. When an acid dissociates, it releases a proton to make the surrounding solution acidic. However, weak acids only partially dissociate and at equilibrium coexist in a deprotonated state (A-) and a protonated state (HA), according to the equation HA ⇌ H+ + A-. The concentration ratio of products and reactants is constant given fixed conditions and is called the acid dissociation constant (Ka). Ka is defined by the equation below. Ka = [H+][A-]/[HA]
ACID IONIZATION CONSTANT or ACID DISSOCIATION CONSTANT
Ka equation
Ka = [H+][A-]/[HA] The square brackets indicate the concentration of the respective aqueous species. Ka expresses how easily an acid releases a proton (i.e. its strength). In addition, this equation shows how the dissociation state of weak acids vary according to the [H+] level in the solution. A commonly tested family of acids on the MCAT are carboxylic acids (those containing –COOH), such as lactic acid and amino acids, which normally have a Ka of approximately 10-3 to 10-6. As this shows, expressing acidity in terms of the Ka constant alone involves inconvenient numbers that are not very intuitive.
pka
Therefore, pKa was introduced as an index to express the acidity of weak acids, where pKa = -logKa. For example, the Ka values for lactic acid (HC3H5O3) and nitrous acid (HNO2) are 8.3 × 10-4 and 4.1 × 10-4, respectively. The pKa values for these acids are 3.1 and 3.4, respectively, which are simpler expressions that are easier to understand and compare. The smaller the pKa value, the stronger the acid (since as X increases, pX decreases). Therefore, the pKa values above tell us that lactic acid is a stronger acid than nitrous acid.
pka for diprotic
For diprotic amino acids (i.e. those amino acids for which the side chain is neither acidic nor basic), the pI can straightforwardly be captured as the average of the two pKa values.
pka for triprotic
For triprotic amino acids (i.e. those that have an acidic or basic side chain), the pI can be obtained by averaging the two acidic pKa values for acidic amino acids or the two basic pKa values for basic amino acids. Another way of saying this is that for acidic amino acids, the pI is the average of the two lowest pKa values; for basic amino acids, the pI is the average of the two highest pKa values. Be careful to avoid averaging all three values given; the pI is always the average of two, not three, pKa values.
buffer 1
Acid-base buffers confer resistance to a change in the pH of a solution when hydrogen ions or hydroxide ions are added or removed to solution. An acid-base buffer typically consists of a weak acid and its conjugate base. ***The most important buffer to know for the MCAT is the bicarbonate buffer system, which is shown below. H2O (aq) + CO2 (g) ⇌ H2CO3 (aq) ⇌ H+ (aq) + HCO3− (aq) Buffers resist pH changes best when the pH values are at or near the pKa value for the acid/base used, because that is when the conjugate acid and base have equal concentrations. Optimal buffering occurs when the pH is within approximately 1 pH unit from the pKa value of the system. The pH of a buffer solution can be calculated using the Henderson-Hasselbalch equation: pH = pKa + log [conjugate base] / [acid].
bicarbonate buffer system
***The most important buffer to know for the MCAT is the bicarbonate buffer system, which is shown below. H2O (aq) + CO2 (g) ⇌ H2CO3 (aq) ⇌ H+ (aq) + HCO3− (aq) Carbonic acid (H2CO3) has the conjugate base of HCO3−. Buffers work because the concentrations of the weak acid and its salt are large compared to the number of protons or hydroxide ions added or removed. When protons are added to the solution from an external source, some of the bicarbonate in the buffer is converted to carbonic acid, using up the protons added; when hydroxide ions are added to the solution, protons are dissociated from some of the carbonic acid in the buffer, converting it to bicarbonate and replacing the protons lost.
bicarbonate buffer system 2
On Test Day, you may see the bicarbonate buffer concept tested from a chemical, biochemical, or biological perspective. For example, hyperventilation (rapid shallow breathing) results in excess CO2 being expelled from the blood, causing the pH to rise. In response, the buffer needs to release more H+ to lower the pH back to physiological norms. An additional fact to be aware of is that other mechanisms in the body are also used to regulate pH, since carbonic acid works best at a pH below physiological conditions, because its pKa1 (pKa1 = 6.3, pKa2 = 10.3) is much lower than the normal pH of blood (7.4).
What is the approximate pH of a saturated aqueous solution of hydrochloric acid whose molarity is 10.6 M?
= -1 Hydrochloric acid is a strong acid and completely dissociates in aqueous solution. In this solution, the hydronium ion concentration is 10.6 M, which can be approximated as 10 M to make the math easier. The pH is the -log of the hydronium ion concentration: -log[10] = -log[101] = -1. While the typical pH range is normally thought of as ranging from 0 to 14, if the concentration of hydronium ion is greater than 1 M, negative pH values are possible. It is also possible to have pH values greater than 14, i.e. if the hydroxide concentration is greater than 1 M.
How acidic or basic a solution is can be expressed in terms of pH or pOH……..
are defined as follows: pH = −log [H+] and pOH = −log [OH−]. For example, a solution with an H+ concentration of 10 ^−4 M will have a pH of 4, and a solution with an OH− concentration of 10^−9 M will have a pOH of 9. pH and pOH values can be estimated given a certain concentration using the following shortcut: p(N × 10−M) = (M−1).(10−N), such that a solution with an H+ concentration of 4 × 10−8 will have a pH = (8−1).(10−4) = 7.6.
Kw
pH and pOH are related to each other through the equation pH + pOH = pKw, where Kw is the autoionization constant of water (Kw = [H3O+][OH−] = 1 × 10−14 at 25°C). Thus, at 25°C, pH + pOH = 14. Thus, a solution with a low pH will automatically have a high pOH, and vice versa. pH is most commonly used, but it is important to be able to interconvert pH and pOH values if needed.
Acidic solutions have a high …………
Acidic solutions have a high H+ concentration and a low pH.
Basic solutions have a low…..
Basic solutions have a low H+ concentration and a high pH.
Bronsted Lowry Acid
proton donor
Bronsted lowry base
proton acceptor
lewis acid
electron pair acceptor
lewis base
electron pair donor
Take B, flip it get D, nice way to remember electron donor******
lewis acid/base
no H plus moving, definition more broad!!
strong acid
100% ionization, donate protons very easily** say process occurs 100% so 100% ionization, equilbirum so far to the right one arrow going right* everything turns into our products!
ex HCl
H2O + HCl –> H3O+ and Cl-
Ka= [H3O+] X [Cl-]/ [HCl] leave out water** is a pure liquid concentration doesnt change so LEAVE IT OUT of equilbirum expression**, super strong number in numerator and small number in denomatinor, so gives you a very big/high number of Ka, Ka much much greater than 1 here* so that is how we recognize a strong acid, an acid ionization constant much much greater than 1**
titration 2
definition
procedure for determining concentration of a solution**
equilbirum expression
Concentration of products/ concentration of reactants
stronger acid….
weaker conjucate base, so Cl- is a weak conjugate base!
H2O+ HCl–> Cl- + H3O+, Cl- weak conjugate base
can think about competing base strength Bronsted Lowrey base water here accepting proton, Cl- anion tries to pick up proton from hydronium (H3O+) for reverse reaction BUT since HCl so good at donating ions Cl- not good at accepting
water much stronger base than chloride anion*
acetic acid
CH3COOH bronsted lowrey acid
H2O BLB
CH3COOH + H2O–> (eq arrows) CH3COO- + H3O+
gives us acetate anion (CH3COO-) plus H3O+**
WEAK ACID don’t donate protons very well, so acetic acid will stay mostly protonated so when think about this reaction coming to an equilbrium will have a high concentration of reactants here**
Ka= [CH3COO-] [H3O+]/ [CH3COOH]
so very small number on top/ large bottom
small number divide by large number gives you Ka value much less than 1* so this value will be much less than 1, and that is how we recognize a weak acid look at Ka value**
autoionization constant for water
Kw, autoionization constnat or ion product ocnstant so not Ka*
H2O + H2O-> H3O+ + OH-
Kw= products/reactants, but dont worry about reactants because pure water so = [H3O+] [OH-]
= 1.0 X 10^-7 M (concentration of hydronium numbers, H3O+) concentration of hydroxide at 25 degrees celcius of pure water is 1.0 X 10^-7
Kw= 1.0 X 10 ^-14, since much less than 1 equilbirum lies far to the left, why have such low concentration of ions***
concentrations of hydronium equal to concentration of hydroxide [H3O+]= [OH-] water neutral*** so solution neutral
H3O+ > OH-
acidic solution
[H3O+]=[OH-]
neutral
[H3O+] < [OH-]
basic
Lemon juice ex. H3O+= 2.2 X 10^-3 M, OH-?
2.2 X 10^-3 M X = 1.0 X 10^-14
because [H3O+][OH-]= 1.0 X 10^-14
x=OH-= 4.5 X 10^-12 M, concentration of H3O+ is greater than concentration of OH-, so this is an acidic solution, ex lemon juice is acidic
ph of water
-log [H3O+]
pH H2O, -log (1.0 X 10^-7)
pH= 7.00 NEUTRAL
or if pH = 3.82, 3.82= -log [H3O+]
to solve that 10^-3.82 = 1.5 X 10^-4 concentration of hydronium ions, if get two significant figures here, need two significant figures for our answer
how to get concentration of H3O+
10^-ph***
calculate the pH of an aq ammonia solution with a [-OH] of 2.1 X 10^-3 M
want us to find pH, which equals - log[H3O+]
BUT they gave us the concentration of -OH, so use the equation [H3O+][-OH] = 1.0 X 10^-14**
plug in, X (2.1 X 10^-3) = 1.0 x 10^-14
so X, the H3O+ concentration is 4.8 X 10^-12. , so use that number to calculate pH
pH= -log (4.8 X 10^-12)= 11.32, so 2 significant figures in log so 2 sig figs to right of decimal point, pH>> 7 its basic!
what is pOH equal to?
pH= -log (H+) or -log(H3O+)
pOH= -log[-OH]
pOH of water
calculate the pH of an aq ammonia solution with a [-OH] of 2.1 X 10^-3 M cnt. 2
pOH= -log (1.0 X 10^-7) same as did for pH above, so pOH= 7.00
remember pH + pOH = 14
ex if pOH= -log(2.1 X 10^-3)
pOH= 2.68, so pOH is 2.68 once again 2 sig figs in 2.1 log so 2 sig figs after decimal place, sovle for pH so the pH plus POH= 14, so 14-2.68 gives us 11.32=pH same pH got when used it a different way so doesnt matter when calculate ammonia solution same anser either way*
pKa
= - logKa
HF
hydrofluoric acid
Ka=3.5 X 10^-4
WEAK ACID, less than 1* greater than acetic acid (Ka 1.8 X 10^-5) and methanol 2.9 X 10^-16
largest value for Ka, but smaller value pKA lower value for pKa more acidic your acid***
methanol
weak base equilbrium
Kb
acid will be BLAcid ammonia will be BLB Nh3, protonate ammonia form ammonium ion, NH4+ and-OH
so if ammonia functioned as bl base, so ammonium conjugate acid to Nh3, water was blacid so conjugate base is -OH
formula
B+ H2O–> -OH + BH
Kb= base dissociation constant, base ionization constant
products over reactanst! [BH][-OH]/ B * reactants leaving out water!
Kb 2
higher value for Kb stronger base, more of your products you will make here***
weak bases
Nh3 ammonia
C6H5NH2 aniline, ammonia KB 1.8 X 10^-5
aniline is 4.3 X 10^-10, so ammonia stroner base than aniline even though both weak bases
pKb= -log Kb= -log (1.8 X 10^-5)
pKb= 4.74
calculate pH of 0.500 M solution of NH3 aq
NH3 + H2O– [NH4+] + -OH
NH3 NH4+ -OH
I 0.500 0 0
C -x +x +x
E 0.500- x x x
- 8 X 10^-5 = (x)(x)/0.5000 -x x<<< 0.500
- 8 X 10^-5 = x^2/0.500
x= 0.0030 M, x refers to OH concentration** hydroxide anions
find pOH= -log (OH- ions concentration) = 2.52, pH+ 2.52 = 14.00
pH= 11.48
Kw
equilbirum constant for net reaction, add rxn together to get net reaction multiple equilbirum constants to get net equ constant
Ka X Kb = Kw
Kb for methylamine is 3.7 X 10^-4, calculate Ka value for the methlyammonium ion
Ch3NH2 is the methylamine
Ch3NH3” methylammonium ion
Ka X Kb = Kw
Ka X (3.7 X 10^-4)= 1.0 X 10^-14
Ka= 2.7 x 10^-11
Kb for methylamine is 3.7 X 10^-4, calculate Ka value for the methlyammonium ion
part 2 (further step)
Ka X Kb = Kw
logKa X Kb = log Kw
-logKa + -logKb = -logKw
pKa + pKb = 14.00
if pKa is =-log (2.7 X 10^-11) (from part 1)
pka = 10.57 (2 sig figs becuase 2.7 2 sig figs) pka of methylammonium ion, asks for pKb for methlamine
to find pkb use equation–> 10.57 + pKb= 14.00, so pKb = 3.43
so this is the relatonship btw Ka and Kb**
calculate the pH of a solution that is 1.00 M Ch3COOH (Ka = 1.8 X 10^-5) and 1.00 M Ch3COONa
common ion effect problem
CH3COOH + H2O –> H3O+ + CH3COO-
anothre source for acetate anions with CH3COONa acetate anion comes from two sources one ionization of acetic acid, other is sodium acetate add in to create solution
at equilbirum would have: look in picture, can write equilbirum expression using Ka becuase acetic acid donating proton to water
Ka= [H3O+]X [CH3COO-]/ CH3COOH
notice in picture gaining acetate anion concentration so add in 1.00 to products** becuase dealing with CH3COONa
*1.00 + x and 1.00-x close to 1 since x<<1.00
*remember x represents concentration of hydronium ions* so for pH =-log(1.8X 10^-5)= 4.74
acetic acid only 1.00 M Ch3COOH pH= 2.38, different pHes pH higher for two sources again for acetate ion, with addition of sodium acetate and acetic acid
acetic acid common ion problem
part 2
Calculate the pH of a solution that is 0.15 M NH3, Kb= 1.8 X 10^-5 and 0.35 NH4NO3
ammonia= weak base, takes proton from water**
equation: NH3 + H2o–> NH4+ + -OH
so ammonium nitrate is another source of NH4+** that also gets an inc in concentration of 0.35 in ICE diagram
ammonium two sources so it is a common ion*
so after ICE step 2: Kb= [NH4+][-OH]/ NH3
Kb= (0.35 + x) (x) / (0.15 -x) if x<<<1.00, x is an extremely small number so can get rid of it
1.8 X 10^-5=(0.35) x/0.15
x (x is the -OH concentration)= 7.7 X 10^-6 M
step 3, to calculate pH, pOH= -log (7.7 X 10^-6), pOH= 5.11
pH+ pOH= 14.00
pH+ 5.11= 14.00
pH= 8.89
find concentration of acidic solution (the solute)
In a titration, 27.4 mL of a 0.0154 M solution of Ba(OH)2 is needed to neutralize 20.0 mL of HCl. What was the concentration of the acid solution?
barium hydroxide concentration = 0.0154 M, molarity = mol/L
Step 1.
0.0154 = X/ 0.0274 L
x= 4.22 X 10^-4 or 0.000422 mol of barium hydroxide Ba(OH)2
Step 2.
now Ba(OH)2 + HCl–> H2O + BaCl2- ions are Ba 2+ and Cl-1
Ba 2+ corses with Cl-1 so BaCl2
balance equation= Ba(OH)2 + 2 HCl –> 2 H2O + BaCl2
mole ratio for Ba(OH)2 to HCl, so for every 1 mol of Ba(OH)2 we have 2 mols of HCl so we know we need 0.000422 mol of Ba(OH)2 needed in our concentraton, so we had twice as many of HCl
so one way: 0.000422 mol X 2= HCl M
or ratio
Ba(OH)2/ HCl = 1/2 = 0.000422/ x
get x = 0.000844 mol of HCl we have at our equivalence point
Step 3.
now just calculate concentration of acid solution
[HCl] = 0.000844 moles / 0.0200 L (the 20.0 mL started with)
HCl= 0.0422 M
titration of a strong acid with a strong base 2
what is pH if add 10.00 mL of 0.500 M NaOH?
we know base adding, OH- ions will neutralize hydronium ions alreayd present, so calculate first how many mols of H3O+ ions are present
conver 20.00 mL to L, 0.0200 L
H3O+= 0.500 M, since Molarity = moles /L
0.500 M= mol/ 0.0200 L = mol= 0.0100 H3O+
step 2. add NaOh strong base, concentration same as OH- ions since strong base, so 0.500 M of NaOH is the same for OH- concentration, convert 10 mL to liters
[-OH]= 0.500 M= mol/ 0.010 L
solve for moles! 0.500 X 0.010 = 0.005 moles of hydroxide ions we have
step 3. so found moles of both acid and base, neutralization reaction that occurs H3O+ + OH –> H2O + H2O
know started with 0.0100 M of H3O+ and added 0.005 M of OH-
all OH- will react and neutralize same amount of hydronium ions, so going to loose all of our OH ions because base will completely react with acid!
H3O+ + OH—>
- 0100 0.00500
- 0.00500 - 0.00500
___________________
=0.00500 mol and 0
left w/ zero moles of our base!
so 0.0100- 0.005= 0.005 so that is how many moles of H3O+ are left over; we have neutralized half of H3O+ present, so another half left over! 1/2 of acid neutralized so 1/2 of acid left!
new concentration of H3O+ in solution = mol/L
= 0.0050 mol/ .030 L = [H3O+] = 0.17 M
****new volume added 10 to 20.00mL= 0.03 L
How does a buffer work?
Buffer, as we have defined, is a mixture of a conjugate acid-base pair that can resist changes in pH when small volumes of strong acids or bases are added.
- When a strong base is added, the acid present in the buffer neutralizes the hydroxide ions (OH-)
- When a strong acid is added, the base present in the buffer neutralizes the hydronium ions (H3O+)
ex. When a strong acid is added, (buffer contains acetic acid and conjugate base acetate ion) the acetate ions neutralize the hydronium ions producing acetic acid (which is already a a component of the buffer)
on the other hand, when a strong base is added, acetic acid consumes the hydroxide ions producing acetate ions (which is also already a constituent of the buffer).
Suppose we have a buffer that contains a weak base NH3, and its conjugate acid, ammonium ion NH4+ ….
When a strong acid is added, ammonia neutralizes the hydronium ions producing ammonium ions (which is already a component of the buffer).
On the other hand, when a strong base is added, ammonium ions consume the hydroxide ions producing ammonia (which is also already a constituent of the buffer).
Buffering system of blood
Maintaining a constant blood pH is critical for the proper functioning of our body.
The buffer that maintains the pH of human blood involves a carbonic acid **** H2CO3 - bicarbonate ion HCO3- system!
When any acidic substance enters the bloodstream, the bicarbonate ions neutralize the hydronium ions forming carbonic acid and water. Carbonic acid is already a component of the buffering system of blood. Thus hydronium ions are removed, preventing the pH of blood from becoming acidic.
On the other hand, when a basic substance enters the bloodstream, carbonic acid reacts with the hydroxide ions producing bicarbonate ions and water. Bicarbonate ions are already a component of the buffer. In this manner, the hydroxide ions are removed from blood, preventing the pH of blood from becoming basic.
ex titration of a strong acid with a weak base
Suppose our analyte is hydrochloric acid HCl (strong acid) and the titrant is ammonia NH3 (weak base). If we start plotting the pH of the analyte against the volume of NH3 that we are adding from the burette dropwise
h3O+ slowly starst getting consumed by NH3, analkyte is still acidic due ot predominance of H3O+ ions.
Point 3: This is the equivalence point (halfway up the steep curve). At this point, moles of NH3 = moles of HCl in the analyte. The H3O+ ions are completely neutralized by NH3. But again do you spot a difference here??? In the case of a weak base versus a strong acid, the pH is not neutral at the equivalence point. The solution is in fact acidic (pH ~ 5.5) at the equivalence point. Let’s rationalize this.
At the equivalence point, the solution only has ammonium ions NH4+ and chloride ions Cl-. but again if you recall the ammonium ion NH4+ is the conjugate acid of the weak base NH3. So Nh4+ is a relatively strong acid (weak base NH3 has a strong conjugate acid) and thus NH4+ will react with H2O to produce hydronium ions making the solution acidic.
After the equivalence point, NH3 addition continues and is in excess, so the pH increases. NH3 is a weak base so the pH is above 7, but is lower than what we saw with a strong base NaOH (case 1).
titration curve for weak acid weak base
ex titration curve of weak acid strong base
1 M of a weak acid HZ with a Ka = 10e-8 equilibrates in water according to the equation NZ + H2O –> H3O+ + Z-.
What is the pH of the solution at equilibrium?
Q. 8 Qbank BP 11-25
A student needs to make a buffer solution at a pOH of 4.80. Of the following acids, the student should use:
A.
hydrocyanic acid (Ka = 6.2 × 10-10).
B.
hypochlorous acid (Ka = 3.5 × 10-8)
C.
acetic acid (Ka = 1.8 × 10-5).
D.
hydrofluoric acid (Ka = 7.2 × 10-4).
A. hydrocyanic acid (Ka = 6.2 × 10^-10). CORRECT
To manufacture a buffer, an acid should be selected with a pKa as close to the desired pH as possible. However, watch out – this question asks about a pOH of 4.80, which is a pH of 9.20. Also, the given values are Kas, not pKas. To convert, remember that pKa = -log(Ka). We can estimate negative logs by finding the values that each of these Kas falls between. For hydrocyanic acid, 6.2 × 10^-10 is between 1 × 10^-10 and 1 × 10^-9, making its pKa between 9 and 10.
B.
hypochlorous acid (Ka = 3.5 × 10-8)
The pKa for this acid lies between 7 and 8, which is best suited for a buffer solution with a pOH between 6 and 7.
C.
acetic acid (Ka = 1.8 × 10^-5).
wrong b/c -this would be best acid to make a buffer at pH 4.80, but the question asks about pOH.
D.
hydrofluoric acid (Ka = 7.2 × 10^-4).
wrong b/c- The pKa for this acid lies between 3 and 4, which is best suited for a buffer solution with a pOH between 10 and 11.
