Discrete random variables Flashcards
(33 cards)
Define a discrete random variable
A random variable that can only take certain values in a finite or countable set
Define the probability mass function of a DRV
p(x) = P(X=x)
State two properties of pmfs
1) all p(x) ≥ 0
2) Sum of all p(x) = 1
Define the kth moment of X
E(Xk)
Similarly, the kth moment of X about a is E((X-a)k) (where a is a real number)
Give the expectation of E(XY) if X and Y are independent
E(XY) = E(X)E(Y)
Note: this property does not prove independence
Define the case for when rvs X and Y are independent
if P(X=x,Y=y) = P(X=x)P(Y=y) for all x and y, X and Y are independent
Give and describe Chebyshev’s inequality

Give and describe the weak law of large numbers
This law demonstrates that the long-run average of a random variable is very unlikely to be far from its expectation, as the variance of the long-run average gets smaller and smaller.
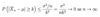
State the expectation of the Bernoulli distribution
p, where p is the probability of success
State the variance of the Bernoulli distribution
p(1-p), where p is the probability of success
Describe the Bernoulli random variable X and give the proper notation
X is defined as the number of successes we have if we perform the experiment.

Describe the Binomial random variable X and give its proper notation
X is defined as the number of successes we have counted after n independent Bernoulli trials have taken place
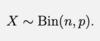
Give the probability mass function of the Binomial distribution
Note that the cdf for the binomial distribution is the sum of the individual probabilities.

State the E(X) for the binomial distribution
np
State the Var(X) of the binomial distribution
np(1-p)
Describe the geometric random variable X and give its proper notation
X is defined as the number of independent Bernoulli trials with the same probability of success up to and including the first success. X* may be used to denote “the number of failures until the first success”, and X* = X - 1

Give the pmf for the geometric distribution

State the E(X) for the geometric distribution

State the Var(X) of the geometric distribution

Describe the Poisson random variable X and give the proper notation
X is defined as the number of events we had recorded on one such surface we had available

Give the pmf for the poisson distribution

State the E(X) of the poisson distribution

State the Var(X) of the Poisson distribution

Describe how the Poisson distribution can be used to approximate the binomial distribution
- This applies if n is large, p is small and np is moderate
- μ = np










