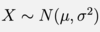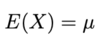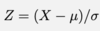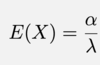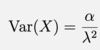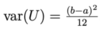Continuous Random Variables

Question 1

Define a continuous rv

Answer 1

A random variables that has an infinite amount of outcomes. Note that probability is assigned to a range, the probability of any given value = 0

Question 2

Define a probability density function

Answer 2

A pdf is a function f that satisfies:

Question 3

Define the cumulative distribution function F

Answer 3

note that we can find f(x) from F(x) by differenting

Question 4

Give four properties of the cdf

Answer 4

Question 5

Give E(X) if X is a crv

Answer 5

Note: the integral must be < ∞

Question 6

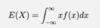
State the E(Y) if Y = g(X)

Answer 6

Question 7

Give Var(X) if X is a crv

Answer 7

Note that the standard deviation is the positive square root of the variance

Question 8

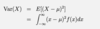
Give four properties of expectation and variance

Answer 8

Question 9

Define the median of a crv

Answer 9

Question 10

Define the mode of a crv

Answer 10

This can be found by finding the stationary points of the pdf

Question 11

Define the case for which two crvs, X and Y, are independent

Answer 11

Note that E(XY) = E(X)E(Y) still holds for crvs

Question 12

Give the formulae for the moment generating function, M(t)

Answer 12

Question 13

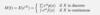
Describe how to obtain E(X^k) using the mgf

Answer 13

Question 14

Give the mgf of Y where Y = aX + b, given that X has mgf M_x(t)

Answer 14

Question 15

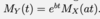
Give the proper notation of the uniform distribution over the interval a,b

Answer 15

Question 16

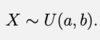
Give the pdf of a uniformly distributed crv over the interval a,b

Answer 16

Question 17

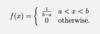
State the E(X) of the uniform distribution over the interval a,b

Answer 17

Question 18

Describe the exponential random variable and give its proper notation

Answer 18

X is defined as the continuous time or interval in space until the first event takes place

Question 19

Give the CDF of the exponential distribution

Answer 19

Question 20

Give the pdf of the exponential distribution

Answer 20

Question 21

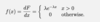
State the E(X) of the exponential distribution

Answer 21

Question 22

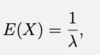
State the Var(X) of the exponential distribution

Answer 22

Question 23

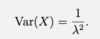
Give the pdf of the gaussian distribution

Answer 23

Note: the Gaussian distribution is the same as the normal distribution

Question 24

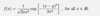
Give the proper notation for the normal/gaussian distribution

Answer 24

Question 25

State E(X) for the gaussian distribution

Answer 25

Question 26

State Var(X) for the Gaussian distribution

Answer 26

Question 27

State the parameters of the standard normal distribution

Answer 27

µ = 0 σ² = 1

Question 28

Give the pdf for the standard normal distribution

Answer 28

Question 29

Give the cdf of the standard normal distribution

Answer 29

Question 30

Give Z such that X_~N(µ,σ²) and Z_~N(0,1)

Answer 30

This is the equivalent to Z = (X-µ)/σ/√n

Question 31

Give the equivalent of Φ(-z) due to symmetry

Answer 31

1-Φ(z)

Question 32

Describe the central limit theorem

Answer 32

The sum of a large number of independent and identically distributed random variables from any distribution is approximately normally distributed.

Question 33

Describe the gamma random variable and give its proper notation

Answer 33

When there is a rate λ \> 0 of rare events per unit of time or space, X is defined to be the continuous interval of time or space until the α-th event takes place, where α is a positive integer. Note that the gamma distribution is the continuous analogue of a Negative Binomial rv α is known as the index or shape parameter λ is known as the scale parameter, or the 'parameter'

Question 34

Define the gamma function Γ(.)

Answer 34

Question 35

Give the pdf of the gamma distribution

Answer 35

Question 36

State E(X) for the gamma distribution

Answer 36

Question 37

State the Var(X) of the gamma distribution

Answer 37

Question 38

State the Var(X) of the uniform distribution

Answer 38