Data Structures & Algorithms Flashcards
Swift collection protocols
“Tier 1, Sequence: A sequence type provides sequential access to its elements. This axiom comes with a caveat: Using the sequential access may destructively consume the elements.
Tier 2, Collection: A collection type is a sequence type that provides additional guarantees. A collection type is finite and allows for repeated nondestructive sequential access.
Tier 3, BidirectionalColllection: A collection type can be a bidirectional collection type if it, as the name suggests, can allow for bidirectional travel up and down the sequence. This isn’t possible for the linked list, since you can only go from the head to the tail, but not the other way around.
Tier 4, RandomAccessCollection: A bidirectional collection type can be a random access collection type if it can guarantee that accessing an element at a particular index will take just as long as access an element at any other index. This is not possible for the linked list, since accessing a node near the front of the list is substantially quicker than one that is further down the list.
Performance analysis of linked list
Explain linked list
It has head
It has tail
Unidirectional
Methods:
push: Adds a value at the front of the list.
append: Adds a value at the end of the list.
insert(after:): Adds a value after a particular node of the list.
After adopting Sequence and Collection gets:
push
append
insert(after:)
pop
removeLast
remove(after:)
Has copy-on-write value semantic (COW) that use isKnownUniquelyReferenced
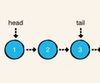
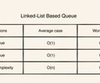
Linked-list queue strengths and weaknesses and Complexity table
Despite O(1) performance, it suffers from high overhead. Each element has to have extra storage for the forward and back reference. Moreover, every time you create a new element, it requires a relatively expensive dynamic allocation. By contrast, QueueArray does bulk allocation, which is faster.
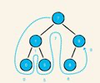
In-order traversal
Pre-order traversal
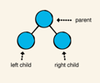
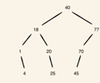
Explain Binary Search Tree
two rules on the binary tree:
The value of a left child must be less than the value of its parent.
Consequently, the value of a right child must be greater than or equal to the value of its parent.
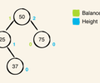
Lookup, insertion and removal is O(log n) if tree is balanced
The binary search tree is a powerful data structure for holding sorted data.
Elements of the binary search tree must be comparable. This can be achieved using a generic constraint or by supplying closures to compare with.
The time complexity for insert, remove and contains methods in a BST is O(log n).
The performance will degrade to O(n) as the tree becomes unbalanced. This is undesirable, so you’ll learn about a self-balancing binary search tree called the AVL tree
Graph analysis matrix vs list
Types of time complexity
Constant time, O(1)
logarithmic time, O(log n)
linear time, O(n)
quasi-linear time O(n log n)
quadratic time O(n2)
If you try to add new elements to an array that is already at maximum capacity
Array must restructure itself to make more room for more elements. This is done by copying all the current elements of the array in a new and bigger container in memory. However, this comes at a cost; Each element of the array has to be visited and copied.
Explain queues
“Array-based
Linked list
Ring buffer
Stack based”
Deque
Common operations for queue:
enqueue: Insert an element at the back of the queue. Returns true if the operation was successful.
dequeue: Remove the element at the front of the queue and return it.
isEmpty: Check if the queue is empty.
peek: Return the element at the front of the queue without removing it.
Array-based queue strengths and weaknesses and Complexity table
Can be inefficient for very large queues
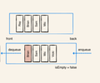
Ring buffer implementation
if read & write is at the same index -> it means that queue if full or empty
fixed size
Double-stack implementation
Dynamic
dequeue is amortised O(1)
Array elementts are next to each other in memory blocks -> loaded in a cache.
Array require O(n) for copy, but it’s very fast O(n)
Compared to other data structures, leveraging two stacks improves
the dequeue(_:) time complexity to amortized O(1) operation.
double-stack implementation beats out Linked-list in terms
of spacial locality.
Space complexity: Array vs linked list queues
Elements in an array are laid out in contiguous memory blocks, whereas elements in a linked list are more scattered with potential for cache misses.
Post-order traversal
Explain Adjacency matrix graph
uses a square matrix to represent a graph
good for dense graphs, when your graph has lots of edges
Objects of graph
Vertex
Edge
Time complexity
“is a measure on the time required to run an algorithm as the input size increases.”
Space complexity
is a measure of the resources required for the algorithm to run.
Big O notation is used to represent
the general form of time and space complexity.
Time and space complexity are
high-level measures of scalability; they do not measure the actual speed of the algorithm itself.
For small data sets, time complexity is usually
irrelevant. A quasilinear algorithm can be slower than a linear algorithm.
Types of Data Structures & Algorithms complexities
Time complexity
Space complexity
How much memory an array takes?
Underneath the hood, Swift arrays are allocated with a predetermined amount of space for its elements.
Array vs Dictionary operations and time cost
If you find yourself needing to use insert(at:) frequently with indices near the beginning of the array
you may want to consider a different data structure such as the linked list.”
Copy-on-write behavior
head first complexity insertion for array and list
Linked lists have a O(1) time complexity for head first insertions. Arrays have O(n) time complexity for head-first insertions
runner’s technique
One is running x2 and when he reaches the end of the list, the slower runner will be in the middle
Finding the middle of list
What to think about when you create new algorithm?
Space complexity -> if you need allocate more objc
Time complexity -> how many objc you need iterate
What ordering queues use?
FIFO first in first out
How blocks of memory placed in linked list vs stack/array
Enqueue vs Dequeue
Enqueue inserts an element to the back of the queue.
Dequeue removes the element at the front of the queue.
Ring-buffer-queue based implementation is good
for queues with a fixed size.
Tree vs linked-list
linked-list nodes may only link to one successor node,
a tree node can link to many child nodes.
Type of traversals
depth-first and level-order
Explain Binary Tree
binary trees that impose restrictions on the insertion/deletion behaviors
AVL Trees explain
It looks like Search Treen, but it balanced itself
Type of balance:
Perfect Balance
Good Balance
Unbalanced
A self-balancing tree avoids performance degradation by performing a balancing procedure whenever you add or remove elements in the tree.
how to measuring balance in AVL tree?
Find height of node and see if left&right child are differ
How AVL balanced itself?
Balance is achieved by four types of tree rotations on node insertion and removal.
How AVL preserve balance?
AVL trees preserve balance by readjusting parts of the tree when the tree is no longer balanced.
Explain Adjacency list graph
stores a list of outgoing edges for every vertex
good for sparse graphs, when your graph has the least amount of edges
