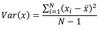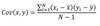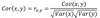Correlations and linear regression Flashcards
(77 cards)
Define
Correlations
Statistical technique for measuring the extent to which two variables are associated Measures the pattern of responses across variables
Define
Linear regression
a linear model to predict the value of one variable from another
Define
One-tailed
a statistical test in which the critical area of a distribution is one-sided so that it is either greater than or less than a certain value, but not both
Define
Two-tailed
a method in which the critical area of a distribution is two-sided and tests whether a sample is greater than or less than a certain range of values
Define
Variance
tells us how much scores deviate from the mean
Define
Covariance
similar to the variance, but tells us how much on two variables differ from their means
Define
Correlation coefficient
The standardised version of covariance
Define
Pearson correlation coefficient
a parametric statistic that measures linear correlation between two variables X and Y. It has a value between +1 and −1.
Define
Correlation matrix
a table showing correlation coefficients between variables
Define
Post hoc
statistical analyses that were specified after the data were seen
Define
Spearman correlation
a nonparametric measure of rank correlation. It assesses how well the relationship between two variables can be described using a monotonic function
Define
Monotonic
relationships that are consistently one-directional
Define
Coefficient of determination (r^2)
the proportion of the variance in the dependent variable that is predictable from the independent variable
Define
Shared variance
the extent to which two variables vary together
Define
Partial correlation
Measures the relationship between two variables, controlling for the effect that a third variable has on them both
Define
Semi-partial (part) correlation
Measures the relationship between two variables, controlling for the effect that a third variable has on one of the others
Define
Zero order correlation
the correlation between two variables when you do not control for anything
Define
Directionality problem
it is not possible to determine which variable is the cause, and which is the effect
Define
Residual
The difference between the observed value of the dependent variable (y) and the predicted value (ŷ)
Definition
Statistical technique for measuring the extent to which two variables are associated Measures the pattern of responses across variables
Correlations
Definition
a linear model to predict the value of one variable from another
Linear regression
Definition
a statistical test in which the critical area of a distribution is one-sided so that it is either greater than or less than a certain value, but not both
One-tailed
Definition
a method in which the critical area of a distribution is two-sided and tests whether a sample is greater than or less than a certain range of values
Two-tailed
Definition
tells us how much scores deviate from the mean
Variance