Continuous Population Dynamics Flashcards
(18 cards)
What is the differential equation associated with exponential growth?
- N(t) individuals
- b per capita birth rate
- d per capita death rate
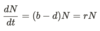
What is the solution to the exponential growth ODE?
- r = growth rate (difference between birth & death rate)
- N_0 = initial population. (Population at t=0)
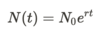
What is a fixed point?
- A fixed point is an equilibrium point, so when the rate of chage (time derivative) of the population is zero:
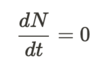
What does the stability of a fixed point mean?
The stability of a fixed point refers to the tendancy of the system to return to the fixed point (or not) after a small perturbation is applied.
If a fixed point is stable, then a small perturbation around the point will cause the system to return back to the fixed point.
If a fixed point is unstable, then a small perturbation around the fixed point will cause the system to move away from the starting value.
What is the logistic growth model?
The logistic growth model is a modification of the exponential growth model by adding a carrying capacity term that limits the maximum population.
This is to acount for resource competition and limitation that would prevent a population from growing exponentially forever.
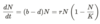
What is the solution to the logistic growth ODE?
The ODE is solved by separating variables and then applying partial fractions to the N term, which obtains the follwing:
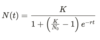
What is the general form of a continous population model used when considering the stability of fixed points?
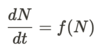
Under what condition is a fixed point said to be feasible?
A fixed point is said to be feasible if it is greater than or equal to zero, this is because the fixed point must correspond to a physical population for the model to make any sense.
What are the general stability conditions for a continous ODE model?

What critieria must be satisfied for a model to demonstrate periodic behaviour?
For a model to be periodic (with period T) the following statements must be true:
- N(t+T) = N(T)
- T is the smallest value for which the above relation holds.
What are some typical rescalings used to introduce dimensionless variables?
- Number of individuals in terms of the carrying capacity.
- Time in terms of the growth rate.
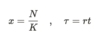
What is the dimensionless version of the logistic growth model?
- Removed parameters from the model so it does not need to be analysed for different carrying capacities and growth rates.

What type of equation is used in delay models?
Delay Differential Equations (DDE’s) are used to model the rate of population change to the current population size, along with the population size at previous times.
These equations have the following general form, where T is the fixed time delay.
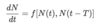
What is the Hutchison-Wright model?
The Hutchison-Wright model is the time delayed version of the logistic equation.
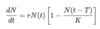
What is the Volterra-Integro equation?
A more general type of DDE depends on many previous times instead of just the population size a fixed time ago. This is provided by the Volterra-Integro differential equation:
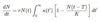
What is the memory kernal?
k(t’) is the memory kernal in a delay differential equation which weights the different historical contributions.
It is also normalised so integrates to 1 between 0 and infinity.
When the memory kernal is a delta function (only valued at one point) then the Hutchison-Wright equation is recovered from the more complex Volterra-Integro equation.
What type of model has the ability to form oscillations?
Delay Differential Equations (DDE’s) have the ability to form oscillations
How is the stability of delay differential equations analysed?
- Find fixed points
- Introduce Small Perturbation
- Linearise equation with respect to the perturbation
- Use trial solution


