Consumption (uncertainty)

Question 1

Consumer’s problem

Answer 1

• In the Euler equation E_t(u_c(c_t+1)) can’t be written as a function of c_t unless u_c is linear

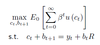
Question 2

Euler equation

Answer 2

All iinformation available at time t to predict c_t+1 is contained in c_t

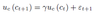
Question 3

Random walk result assumptions

Answer 3

beta*R=1

Question 4

Implications random walk result

Answer 4

• Consumption is equal to permanent income
  
  • permanent income is defined in terms of expectations
• Innovation in consumption is equal to the innovation of permanent income
• Once we control for consumption at time t, all other variables at time t shouldn’t have any predictive power for consumption at period t+1

Question 5

Certainty equivalence property

Answer 5

• Households consume every period the same amount as they would if the income process was deterministic and equal to its mean
• Variance does not matter

Question 6

Excess sensitivity puzzle

Answer 6

• Problem with the empirical implications of the Euler equation
• Current consumption responds to lagged variables in excess of what is predicted by the theory
• Past values of wealth add information to predict consumption beyond the first lag of consumption
• Other authors also find that lagged income helps to predict current consumption

Question 7

Excess smoothness puzzle

Answer 7

• Problem with the empirical implications of the consumption function
• If income is stationary, consumptions changes should be less volatile than income changes
• In income follows a random walk, we should expect about the same size in volatility
• Volatility in changes in aggregate consumption is much lower than the volatility of changes in aggregate income, even though the hypothesis of a unit root for the income process isn’t rejected

Question 8

Precautionary savings def

Answer 8

• Amount of assents held for the sole purpose of smoothing consumption among different states of the world
  
  • Negation of certainty equivalence property

Question 9

Precautionary savings model setup

Answer 9

• Two periods
• Continuum of exante identical agents that face uncertain and uninsurable exogeneous labor income

Question 10

Prudence property

Answer 10

u_ccc(c)>0, i. e. marginal utility is a convex funtion.

• In the partial equilibrium approach, prundence implies that an increase in the variance of consumption increases the amount of precautionary savings.

Question 11

Prudence property implications

Answer 11

• Precautionary savings increase with income untertainty if the marginal utility is convex

Question 12

Hansen Singleton

Answer 12

Reject the model under the lognormality assumption

Question 13

Equity premium puzzle

Answer 13

• Fot the euler equation to be consistent with the time series data on aggregate consumption and returns on stocks and risk free bonds, the degree of risk sversion must be huge