Congruent Polygons Flashcards
(13 cards)
Congruent Polygons
Vertices can be paired such that the corresponding sides and angles are congruent
Triangles: 3 angles of one triangle are congruent to the 3 corresponding angles of the other triangle
3 sides of one triangle are congruent to the 3 corresponding sides of the other triangle
SSS Postulate
If the three sides of one triangle are congruent to the three sides of another triangle, then the two triangles are congruent
ASA Postulate
If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent
SAS Postulate
If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent
AAS Theorem
Converts to ASA
If you know two angles (1 & 2) and a side (3) , you can determine the 3rd angle (4) and have ASA with the new angle (4), the side (3) and whichever old angle is on the other end of the side (2)

CPCTC
Corresponding Parts of Congruent Triangles are Congruent
Altitude
A segment from the vertex that is perpendicular to the (extension of the) opposite side
There are 3 altitudes in one triangle (one from each point of the triangle)

Median
A segment joining the vertex and the midpoint of the opposite side
There are 3 medians in a triangle (one from each point on the triangle)
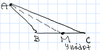
Isosceles Triangle
A triangle with at least 2 congruent sides
(Equilateral triangle is a type of an isosceles triangle)
Isosceles Triangle Theorem (ITT)
Two sides of a triangle are congruent IFF the opposite angles are congruent
Hypotenuse Leg Theorem (HL Theorem)
If the leg and hypotenuse of one right triangle is congruent to the leg and hypotenuse of another right triangle, then the triangles are congruent
Equidistance Theorem
If a point is equidistant from the sides of an angle, then it lies on the angle bisector
Perpendicular Bisector
The locus of points equidistant from the endpoints of the segment it is bisecting


