Alt-On-Hyp, Trip and Similarity Flashcards
1
Q
Geometric Mean
A
x of a and b such that
x2 = ab
2
Q
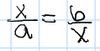
Alt-On-Hyp
A
The altitude to the hypotenuse of a right triangle is the geometric mean of the segments that the hypotenuse is divided into by the alititude
3
Q
Leg-Alt-On-Hyp
A
If we draw an altitude to the hypotenuse of a right triangle, then each leg is the geometric mean of the hypotenuse and the adjacent segment of the hypotenuse
4
Q
sin(x)
A
opposite leg
hypotenuse
5
Q
cos(x)
A
adjacent leg
hypotenuse
6
Q
tan(x)
A
opposite leg
adjacent leg
(slope of the hypotenuse)
7
Q
sin(30°)
A
1/2
8
Q
cos(30°)
A
sqrt(3)/2
9
Q
tan(30°)
A
sqrt(3)/3
10
Q
sin(60°)
A
sqrt(3)/2
11
Q
cos(60°)
A
1/2
12
Q
tan(60°)
A
sqrt(3)
13
Q
sin(45°)
A
sqrt(2)/2
14
Q
cos(45°)
A
sqrt(2)/2
15
Q
tan(45°)
A
1
