Area and Right Triangles and Fundamentals of Proof Flashcards
definition and area postulates
Postulate
Assumption
- If two closed regions intersect only along a common boundary, then the area of their union is equal to the sum of their individual area
- Every closed reagion has an area
- If two closed figures are congruent, then their areas are equal
- The area of a rectangle is equal to the product of the base and the height of that base
area
Square
The area of a square is equal to the length of its side squared.
Asq = s2
s= side
area
Rectangle
Derived from the area of a square:
Arect = ab = bh
b= base
h= height
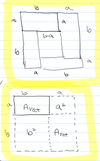
area
Parallelogram
Quadrilateral with opposite sides parallel
Aparallelogram = bh
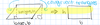
area
Triangle
Atri = 1/2bh
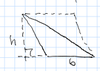
area
Trapezoid
Exactly one pair of parallel sides
Atrap = 1/2[(b1 + b2)h]
area
Rhombus
Quadrilateral with all sides congruent
diagnoals = d1 and d2
Arhom = bh = 1/2(d1d2)
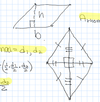
area
Kite
diagnoals = d1 and d2
Arhom = bh = 1/2(d1d2)
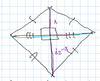
Pythagorean Theorem
The square of the hypotenuse of a right triangle equals the sum of the squares of the two legs
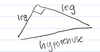
45-45-90 Triangle
Ratio of leg to hypotenuse
1:sqrt(2)
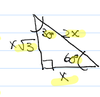
30-60-90 Triangles
Ratio of short leg to long leg to the hypotenuse
1: sqrt(3): 2
Equilateral Triangle Area
A = [s2sqrt(3)]/4
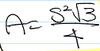
Ratio of Areas of Triangles (TART)
Theorem: The ratio of areas of two triangles equals the product of the ratios of the bases and the ratio of the heights
A1/A2 = (b1/b2)(h1/h2)
corolaaries: if two triangles have equal bases, the ratio of their areas is equal to the ratio of the heights
if two triangles have equal heights, the ratio of their areas is equal to the ratio of the bases
Segment Addition Postulate
PQ + QR = PR whenever Q is between P and R
Midpoint Definition
Point M, in between points A and B, such that AM = MB
Bisector
A line, segment, ray or plane that passes through the midpoint
Angle Bisector
Line/Segment/Ray BX, in the interior of angle ABC such that angle ABX = angle CBX
Angle Addition Postulate
angle ABX + angle CBX = angle ABC where X is in the interior of the angle
Linear Pairs
= 180 degrees
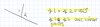
Midpoint Theorem
If M is the midpoint of AB, then AM = 1/2 AB and MB = 1/2 AB
Definition vs. Theorem
the theorem is something deductively proven based on the definition
Vertical Angles
are congruent
Addition/Subtraction Property of Equality
a = b, c = d
a + c = b + d
Multiplication/Division Property of Equality
a = b, c = d
ac = bd
Reflexive Property of Equality
a = a
Symmetric Property of Equality
a = b
b = a
Transitive Property of Equality
a = b, b = c
a = c
Substitution Property of Equality
If a = b, we can replace any occurrance of a with b
Conditional Statements
If [hypothesis], then [conclusion]
Converse of a Statement
Swtich the hypothesis and conclusion
If [conclusion], then [hypothesis]
Biconditional Statements
Combines a statement and its converse
Inverse of a Statement
Negate the statement
If not [hypothesis], then not [conclusion]
Contrapositive
Switch and negate the hypothesis and conclusion
If not [conclusion], then not [hypothesis]
Venn Diagrams
if p, then q
if not q, then not p
if q, then p
if not p, then not q
if p, then q = if not q, then not p
if q, then p = if not p, then not q
Logically Equivalent
Statements that have the same truth value
