Confidence Intervals Flashcards
When should you use a T-Interval?
When estimating for the mean but the population standard deviation is unknown.
When should you use a T-Interval?
When estimating for the mean but the population standard deviation is unknown.
What is the general formula for confidence intervals?
estimate (+ or -) critical value • standard error
Stating population and parameter for a 2-sample t-interval
We will estimate the difference between the means (parameter) of the two samples (population).
Calculating sample size based on a set margin of error
MEAN
ex. 2-sample t-interval
PROPORTION
ex. 1-proportion Z test
Put values given equal to the equation, and solve for n.
ME= t* √(s)/n or z* √σ /n
ex. ME = t* √(s_1^2)/n_1 +(s_2^2)/n_2
ME= √p (1-p)/n
ex. ME= √p (1-p)/n
What are the conditions and assumptions for the T-Interval?
-Simple Random Sample -Normality -Population is normal or N≥30 so Central Limit Theorem applies or given data shows the sample is symmetric with no outliers
What is the formula for the T-Interval?
X ̅ ± t* S/√n
What are the conditions and assumptions for the T-Interval?
-Simple Random Sample -Normality -Population is normal or N≥30 so Central Limit Theorem applies or given data shows the sample is symmetric with no outliers
What is the formula for the T-Interval?
X ̅ ± t* S/√n
when do you use a matched pairs t interval?
when you are estimating the mean difference for a random variable
what are the conditions and assumptions for the matched pairs t interval?
SRS & normality - population is normal, sample is larger than 30 (CLT) or given data is symmetric with no outliers
When do you use a 2-sample t-interval?
When you are estimating the difference between the means of two independent populations, and when sigma (standard deviation) of the populations is unknown.
what are the conditions and assumtions for the 2 sample T interval?
SRS for each sample
Normality ( graph if you have data)
Two independent damples
standard deviation for population is unknown
How do you calculate t* for a confidence interval?
You will need to use the confidence level and the degrees of freedom. Just like when calculating z*, use (area of confidence level+area of one tail), except you use invT. Determine the degrees of freedom (sample size - 1), and then use the calculator for
invT(area, DF) = t*.
This can also be done on the table by using the degrees of freedom and confidence level.
What is the equation for matched pairs t-interval?
estimate +/- t* x standard error
what is the standard error for a matched pairs t interval?
the square root of (standard deviation of the sample / sample size)
How do you calculate for z* in a confidence interval?
To calculate the critical value z*, you will use ‘invNorm’ on the 2nd Vars menu of the calculator (or the table). Let’s take the confidence level of 95 percent. Draw a normal curve, the middle section being 95 percent, then add the value of one tail end. To do this, you would take 1 (the area under the whole curve), subtract 0.95 (the middle of the curve), then divide by two (area of two tails/two= area of one tail). Then you would add that tail value back to 0.95.
1 - 0.95 = 0.05
- 05 / 2 = 0.025
- 025 + 0.95 = 0.975
Then enter this in invNorm.
invNorm(0.975) = 1.9599 = z*
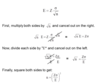
what are the conditions and assumptions for the Z-interval??????????????????
- the data is from a SRS
- the sampling data is approximatly normal
- standard devation is known
what is the formula for the Z-interval?



