Chapter Four: Special Topics

Question 1

equations of a vertical parabola

Answer 1

(x - h)² = 4p(y - k)

y = a(x - h)² + k

note: a = 4p

Question 2

equations of a horizontal parabola

Answer 2

(y - k)² = 4p(x - h)

x = a(y - k)² + h

note: a = 4p

Question 3

where is the focus of a parabola located?

Answer 3

• ±p distance away from the vertex
• y = cx² –> (0, 1/4c)
• x = cy² –> (1/4c, 0)

Question 4

where is the directrix of a parabola located?

Answer 4

• ±p distance away from the vertex (in the opposite direction of the focus)
• y = cx² –> y = -1/4c
• x = cy² –> x = -1/4c

Question 5

how can you determine the axis of symmetry of a parabola?

Answer 5

it is the equation of the horizontal or vertical line through the vertex and the center of the parabola

(ie: if the vertex is (-3, 2) and the parabola opens up, the equation for the axis of symmetry is x = -3)

Question 6

what is the standard equation of an ellipse?

Answer 6

note: the term with the larger denominator comes first

(the larger denominator denotes the major axis)

Question 7

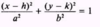
where are the intercepts of an ellipse that has a center of (0, 0)?

Answer 7

the x-intercepts are at ±a

the y-intercepts are at ±b

Question 8

where are the foci of an ellipse?

Answer 8

• if the x term is first –> (±c, 0)
  
  • c² = a² - b²
• if the y term is first –> (0, ±c)
  
  • c² = b² - a²
• c² = larger denominator - smaller denominator

Question 9

what is the equation of a standard hyperbola? what are the intercepts of this hyperbola?

Answer 9

• will never cross y-axis
• x-intercepts at ±a
• foci at (±c, 0)
  
  • c² = a² + b²

Question 10

what is the standard equation of a vertical hyperbola? what are the intercepts and foci of this hyperbola?

Answer 10

• will never cross the x-axis
• intercepts at ±b
• foci at (0, ±c)
  
  • c² = a² + b²

Question 11

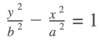
what is the equation for the asymptotes of a hyperbola?

Answer 11

Question 12

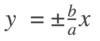
binomial theorem

Answer 12

Question 13

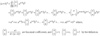
binomial coefficient

Answer 13

Question 14

factorial

Answer 14

n!

the product of all the natural numbers that are less than or equal to n

Question 15

sequence

Answer 15

an ordered collection of numbers, where a_n describes the location of a number in that sequence

Question 16

inductive/recursive sequence

Answer 16

a sequence where the next term depends on the value of the previous term (ex: fibonacci)

Question 17

arithmetic sequence

Answer 17

• a sequence with a constant difference between terms
• a_n = a₁ + (n - 1)d

Question 18

geometric sequence

Answer 18

• a sequence with a constant multiplicative ratio
• a_n = a₁r^n-1
  
  • r = (a_{n + 1})/(a_n)

Question 19

sum of a finite arithmetic sequence

Answer 19

Question 20

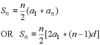
sum of a finite geometric sequence

Answer 20

Question 21

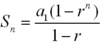
induction

Answer 21

if the first statement is proven true –> the next statement must be true –> all statements are true

Question 22

steps to prove by induction

Answer 22

1. prove that the statement is true for n = 1
   
   • the base case does not have to be for n = 1
2. assume that the statement is true for n = k
3. prove that the statement is true for n = (k + 1)

Question 23

permutation

Answer 23

an arrangement of distinct objects in a definite order

Question 24

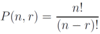
combination

Answer 24

a way of selecting things from a collection when order does not matter

(also the binomial coefficient formula)

Question 25

probability formula

Answer 25

(# of successful outcomes) / (# of total outcomes)

Question 26

multiplicative probability

Answer 26

the probability of two events co-occurring is the product of their individual probabilities

Question 27

additive probability

Answer 27

the probability of two mutually exclusive events occuring is the sum of their probabilities

Question 28

mutually inclusive probability

Answer 28

the probability of two mutually inclusive events occuring is the sum of the two events minus the probability of the inclusive event

(ex: the probability of a red or a queen would be red + queen - red queen)