Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

A-Level Physics > Chapter 9: Energy, Power and Resistance > Flashcards

Chapter 9: Energy, Power and Resistance Flashcards

You may prefer our related Brainscape-certified flashcards:
Physics 101 flashcards AP® Physics flashcards
1
Q
  1. What is a battery?
  2. How are the positive and negative terminals distinguished from each other?
  3. Why should polarity be represented correctly in circuits?
A
  1. A battery means two or more cells connected end-to-end, or in series.
  2. In the case of a single cell or battery, the longer terminal represents the positive terminal. When using a power supply, a small plus sign is often placed next to the positive terminal.
  3. Polarity is very important when using components such as diodes and light-emitting diodes.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

Give the circuit symbols for:

  1. switch (open)
  2. switch (closed)
  3. cell
  4. battery
  5. diode
  6. resistor
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

Give the circuit symbols for:

  1. variable resistor
  2. lamp
  3. fuse
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

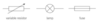
Give the circuit symbols for:

  1. voltmeter
  2. ammeter
  3. thermisor
  4. LDR
  5. LED
  6. capacitor
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q
  1. What is potential difference?
  2. What is potential difference measured in?
  3. Give an alterative definition for potential difference.
  4. What is the defining equation for potential difference?
  5. How is potential difference measured?
  6. What is an ideal voltmeter? Explain.
A
  1. Potential difference is a measure of the transfer of energy by charge carriers.
  2. Potential difference is measured in volt. One volt is the p.d. across a component when 1 J of energy is transferred per unit charge passing through the component.
    1 V = 1 J C–1
  3. Potential difference measures the energy transferred from electrical energy to other forms as charge carriers move through the components per unit charge.
  4. V = W / Q where V is the p.d. measured in volts, Q is the charge in coulombs, and W is the energy transferred by charge Q.
  5. A voltmeter is used to measure p.d. Voltemeters are always connected in parallel across a particular component.
  6. An ideal voltmeter would have infinite resistance, so that when connected, no current passes through the voltmeter itself. Hence, most voltmeters have a resistance of several million ohms.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

Compare potential difference and electromotive force.

A

Potential difference is used to describe when work is done by the charge carriers (charges are losing energy as they pass through the component).
Electromotive force is used to describe when work is done on the charge carriers (charges are gaining energy as they pass through the component).

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q
  1. What does a greater electromotive force represent?
  2. Give examples of sources of e.m.f. and their energy source.
  3. Give the definition of electromotive force.
  4. Give the defining equation for electromotive force.
A
  1. The greater the e.m.f., the more energy per coulomb has been transferred (often from chemical energy in a cell) into electrical energy.
  2. Cells from chemical energy; solar cells from light; dynamos from movement; and thermocouples from heat.
  3. Electromotive force is defined as the energy transferred from chemical energy (or another form) to electrical energy per unit charge.
  4. {curly E} = W / Q where {curly E} is e.m.f measured in volts, Q is the charge in coulombs, and W is the energy transferred by charge Q.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

How can the energy transferred to or from the charges be calculated?

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q
  • What is an electron gun?
    • How can electron guns be used?
  • Describe and explain thermionic emission in electron guns.
  • After thermionic emission, how is a narrow beam of electrons created?
    • How is a beam of electrons achieved?
A
  • An electron gun is an electrical device used to produce a narrow beam of electrons.
    • These electrons can be used to ionise particles by adding or removing electrons from atoms, and they can have very precisely determined kinetic energies.
    • Electron guns are used in scientific instruments, such as electron microscopes, mass spectrometers, and oscilloscopes.
  • The process of thermionic emission involves heating a small metal filament by an electric current. The electrons in this piece of wire gain kinetic energy. Some of them gain enough kinetic energy to escape from the surface of the metal. These electrons are used in the electron gun.
  • The heated filament is placed in a vacuum and a high p.d. is applied between the filament and an anode. The filament acts as a cathode so the freed electrons accelerate towards the anode, gaining kinetic energy.
    • If the anode has a small hole in it, then electrons in line with this hole can pass through it, creating a beam of electrons with a specific kinetic energy.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

In an electron gun, as the electrons accelerate towards the anode they gain kinetic energy. Calculate the equation for work done on a single electron.

A

From the definition for p.d., the work done on a single electron travelling from the cathode to the anode is equal to eV
where e is the elementary charge (charge on each electron) and V is the acceleration potential difference.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

Derive an expression relating the work done on an electron to its increase kinetic energy. What can be concluded from this expression?

EXTENSION: What assumptions did you make?

A

By considering the law of conservation of energy, it can be concluded that

work done on electron = gain in kinetic energy

so e V = 0.5 m v2

The greater the accelerating potential difference, the more energy is transferred to the electrons and so the faster they move.

EXTENSION: This assumes the electrons have negligible kinetic energy at the cathode.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q
  1. Explain the premise of resistance.
  2. How does resistance relate to energy?
  3. How can the resistance of a component in a circuit be determined?
  4. What is the unit of resistance?
A
  1. All electrical components resist the flow of charge carriers through it to some extent, and hence they each have their own resistance
  2. It takes energy to push electrons through a component, and the higher the resistance of that component the more energy it takes.
  3. The resistace of a component in a circuit can be determined by measuring the current I in the component and the p.d. V across the component. The resistance of the component R is defined as the ratio between V and I.
    R = V / I
  4. The unit of resistance is the ohm. The ohm is defined as the resistance of a component when a p.d. of 1 V is produced per ampere of current.
    1 Ω = 1 V A–1
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

What is Ohm’s law?

A

Ohm’s law states that for a metallic conductor kept at a constant temperature, the current in the wire is directly proportional to the p.d. across its ends.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q
  1. Over time, what can happen to the current in a circuit?
  2. Explain this phenomena.
A
  1. The current in a circuit may decrease as the temperature of the wire increases over time as a result of heating caused by the current. As the wire gets hotter, its resistance increases.
  2. When the temperature of the wire increases, the positive ions inside the wire have more internal energy and vibrate with greater amplitude about their mean positions.
    • The frequency of the collisions between the charge carriers (free electrons in the metal) and the positive ions increases, and so the charge carriers do more work/transfer more energy as they travel through the wire.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

Describe and explain the I-V characteristic for a resistor. Comment on the effect of polarity and what can be classified as a resistor.

A
  • The I-V characteristic for a fixed resistor is a straight line through the origin.
    • The potential difference across the resistor is directly proportional to the current in the resistor. As a result
      • a resistor obeys Ohm’s law, and so can be described as an ohmic conductor
      • the resistance of the resistor is constant.
    • The resistor behaves in the same way regardless of polarity.
  • Most wires and other metallic conductors behave in the same way as a resistor; they can be thought of as resistors with very low resistance.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

Describe and explain the I-V characteristic for a filament lamp.

A
  • The I-V characteristic for a filament lamp is not linear.
    • The potential difference across a filament lamp is not directly proportional to the current through the filament lamp. In other words
      • a filament lamp does not obey Ohm’s law, and so can be described as a non-ohmic component
      • the resistance of a filament lamp is not constant.
    • The filament lamp behaves in the same way regardless of polarity.
    • The resistance of the filament increases as the p.d. across it increases. You can confirm this by determining V / I at different points on the graph.
    • This increase in resistance is caused by the wire getting so hot that it glows. The current increasing means that the rate of flow of charge increases through the filament (more electrons pass through it per second) so more collisions occur between the electrons and the positive metal ions per second. When the electrons collide with the ions they transfer energy to the ions, causing the ions to vibrate more and hence increase in temperature.
17
Q

What is special about a diode?

A

A diode only allows a current in one particular direction.

18
Q

What are LEDs?

A

Light-emitting diodes are diodes that emit light of a specific wavelength when the conduct.

19
Q

How are LEDs used in circuits? Why?

A

As LEDs are so efficient and take very little energy to run, they are sometimes used as simple indicators to show the direction of current through a particular part of a circuit. They light up when there is current in them, showing that part of the circuit is live.

20
Q

Describe and explain the I-V characteristic for a diode.

A
  • A diode is made from a semiconductor. Looking at the graph for a semiconducting diode, we can draw a number of conclusions.
    • The potential difference across a diode is not directly proportional to the current through it. This means
      • a diode does not obey Ohm’s law and so can be described as a non-ohmic component
      • the resistance of the diode is not constant.
    • The diode’s behaviour depends on polarity.
  • The resistance of the diode is very high at A – infinite for practical purposes. With the p.d. in this reverse direction, the diode does not conduct.
  • At B, the p.d. increases and the resistance gradully starts to drop. For a silicon diode this happens at around 0.7 V (the threshold p.d.) .
    • Above this value, the resistance drops sharply for every small increase in p.d.
  • Different LEDs have different values for their threshold p.d., which is related to the colour of the light they emit.
21
Q
  1. What does the term resistance refer to?
  2. There are four factors that affect the resistance of a component. What are they?
  3. What does resistivity mean? Give an example.
A
  1. The term ‘resistance’ refers only to a specific component.
  2. The material, the temperature, the length, and the cross-sectional area affect the resistance of a component.
  3. Resistivity is used to describe the electrical property of a material. For example, different components made from copper may have different resistances (due to length or cross-sectional area variations) but copper has a unique resistivity.
22
Q
  1. What is the proportionality between resistance and length?
  2. What is the proportionality between resistance and cross-sectional area?
  3. How can the relationship between resistance, length and cross-sectional area be combined?
  4. What is the constant of proportionality?
  5. What are the units for resistivity?
A
  1. For any given current, increasing the length of the wire will increase the p.d. across it The resistance R of a wire is directly proporitonal to its length L.
  2. When the cross-sectional area of the wire increases, the resistance drops. The resistance R of the a wire is inversely proportional to its cross-sectional area A.
  3. R ∝ L / A
  4. R = ρL / A
  5. Resistivity has the unit ohm metre (Ω m).
23
Q
  1. How can resistivity be defined?
  2. How does the resistivity of a material vary with temperature?
  3. Give the approximate resistivity of conductors, insulators and semiconductors at 20 ˚C.
A
  1. The resistivity of a material at a given temperature can be defined by the rearranged equation ρ = RA / L
    where R is the resistance if a component, A is the cross-sectional area of it, and L is its length.
  2. The resistivity of a material varies with temperature in the same way as the resistance of most components: as the metal gets hotter, its resistivity increases.
    NOTE: the resistivity can also be found by multiplying the gradient [R/L] in a resistance-length graph by the cross-sectional area of the wire.
  3. Good conductors like metals have a resistivity to the order 10–8 Ωm, insulators have a value to the order 1016 Ωm, and semiconductors have values in between these extremes.
24
Q

Describe and explain how some semiconductor components have a negative temperature coefficient.

A
  • Some semiconductors have a negative temperature coefficient, meaning that their resistance drops as the temperature increases.
    • The effect can be explained in terms of the number density of the charge carriers within the material from which the component is made. In some semiconductors, as the temperature increases, the number density of the charge carriers also increases.
25
Q
  • What is a thermistor?
    • Describe and explain the trend.
A
  • A thermistor is an electrical compoent made from a semiconductor with a negative temperature coefficient. As the temperature of the thermistor increases, its resistance drops.
    • The drop in resistance of a thermistor as the temperature increases is not linear — there is often a dramatic drop in resistance, followed by a more gradual decrease as it gets hotter. This makes thermistors particularly useful in temperature-sensing circuits; a small change in temperature can be detected by monitoring the resistance of the thermistor.
26
Q

Where are thermistors used?

A

Thermistors are used:

  • in simple thermometers
  • in thermostats to control heating and air-conditioning units
  • to monitor the temperature of the components inside electrical devices like computers and smartphones so that they can power down before overheating damages them
  • to measure temperature in a wide variety of electrical devices like toasters, kettles, fridges, freezers, and hair dryers
  • to monitor engine temperatures to ensure the engine does not overheat.
27
Q

Describe the water bath experiment.

A
  • A water bath can be used to control the temperature of a thermistor while an ohmmeter is connected directly to the thermistor to measure the resistance at varying temperatures.
    • Alternatively, an ammeter and a voltmeter can be used to measure current in the thermistor and p.d. across it at different temperatures. The resistance can then be found using R = V / I.
  • The results from this experiment may be used in the choice of a thermistor for a particular application. A thermistor is selected to ensure it provides the greatest change in resistance over the range of temperatures in which it will operate.
28
Q

Describe and explain the I-V characteristic for a thermistor. Compare this to the I-V characteristic for a filament lamp.

A
  • Like most semiconducting components, thermistors are non-ohmic.
  • The I-V characteristic has some features that are similar to that of a filament lamp, and one crucial difference.
    • With a thermistor – like a filament lamp – as the current increases, electrons transfer energy to the positive ions, which raises the temperature. But unlike the lamp, this temperature increase leads to a drop in resistance because the number denisty of charge carriers increases. This can be confrimed by comparing R = V / I at various points on the graph.
29
Q
  1. What are LDRs?
  2. What factor is the number density of charge carriers in LDRs determined by?
A
  1. Light-dependant resistors are small electrical components which change their resistance depneding on the light intensity.
  2. A typical LDR is made from a semionductor in which the number density of charge carriers change depending on the intensity of the incident light.
    • In dark conditions, the LDR has a very high resistance. The number density of the free electrons inside the semiconductor is very low, so the resistance is very high.
    • When light shines onto the LDR, the number density of the charge carriers increases dramatically, leading to a rapid decrease in the resitance of this component.
30
Q

How can the effect of light intensity on the resistance of an LDR be investigated?

A
  • The effect of light intensity on the resistance of an LDR can be investigated by varying the distance between an LDR (connected to an ohmeter) and a filament lamp. A narrow tube made of black cardboard can be placed around the LDR to reduce the effect of other background sources of light.
    • The results give a callibration graph that relates the resistance of the LDR to the light intensity. This graph can then be used to determine light intensity from different sources.
31
Q
  1. Define electrical power.
  2. What factors affect the electrical power?
  3. What is the primary equation for electrical power?
A
  1. Electrical power is the rate of energy transfer by each electrical component.
  2. The electrical power depends on the current I in the component and the potential difference V across it.
  3. The equation of electrical power P in watts [W] is
    electrical power = p.d. x current
    P = VI.
32
Q

Derive two alternative equations for electrical power from
P = VI.

A
33
Q

Show the derivation of P = VI.

A
34
Q

Give the derivation for how energy transferred is calculated.

A
35
Q

What is the cost of energy based on?

A

The energy transferred to each individual electrical device, and so how it costs to run, depends on two factors:

  • the power of the device
  • how long the device is used for.
36
Q

How can the energy transferred by an electrical device be determined? Give the proof.

A
  • The defining equation for power is
    power = energy transferred / time taken (P = W/t).
  • Rearranging this equation to determine the energy transferred by an electrical device gives
    W = P t.
37
Q
  1. How does the SI unit for energy and the unit used in electricity bills differ?
  2. What is 1kWh is J?
  3. What is the typical cost of each kWh of electrical energy?
A
  1. The SI unit for energy is the joule (J) but electricity bills use a derived unit, the kilowatt-hour (kWh), defined as the energy transferred by a device with a power of 1kW operating for a time of 1 hour.
  2. 1kWh = 3.6MJ
  3. 6 – 15p

A-Level Physics (9 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions