Chapter 10: Electrical Circuits Flashcards
State Kirchhoff’s second law.
Kirchhoff’s second law takes the law of conservation of energy and applies to electrical circuits. It states that, in any circuit, the sum of the e.m.f.s is equal to the sum of the p.d.s around a closed loop
Describe and explain the current in a series circuit.
- A series circuit has only one path for the current, a single loop from one terminal of the source of e.m.f. back to the other terminal.
- In a series circuit, the current is therefore the same in every position.
- The rate of flow of charge is the same at all points in the circuits because the charge is not used up; it just flows around the circuit (Kirchhoff’s first law).
- In a series circuit, the current is therefore the same in every position.
Describe and explain the e.m.f in a series circuit.
- Kirchhoff’s second law shows that the e.m.f. is shared between components in a series circuit.
- If the circuit contains two components with the the same resistance, the e.m.f. is shared equally between them.
- If the components have different resistances, the component with the greater resistance will take a greater proportion of the e.m.f.
- In circuits with more than one source of e.m.f, the same rule applies, but the e.m.f from each source needs to be added together before sharing between components.
EXAM NOTE: when adding together the e.m.f. from each source, they must be subtracted from each other when the sources are connected with opposing polarities (i.e. negative adjacent to negative).
Summarise the current and p.d. in a parallel circuit.
- A parallel circuit provides more than one possible path for the charges.
- How much charge (current) flows down each branch depends on the resistance of the branch.
- However, the p.d. across each branch is the same as the total e.m.f regardless of how many branches there are.
Describe the flow of current in a parallel circuit. Give an example.
- In terms of current, the greater the resistance of the branch, the lower the current that passes through it.
- For example, if one branch has half the resistance of the other, it will have twice the current flowing through it. Hence, 2/3 of the total current will go through that branch (with the lower resistance).
Describe the relationship between e.m.f and p.d. in a parallel circuit.
- In a parallel circuit, each branch forms its own loop. Kirchhoff’s second law tells us that the e.m.f. around each loop must equal the p.d. around that loop.
- If there is more than one component on a branch, then within that branch, the sum of the p.d.s across each component must equal the e.m.f.
EXAM NOTE: In more complex circuits, it is useful to consider each loop separately, paying particular attention to components in parallel.
Describe and explain the relationship R = R1 + R2 +…
Written Explanation
- When resistors are connected in series, each additional resistor effectively increases the length of the path taken by the charges and hence increases the resistance.
- Therefore, the total resistance R of a number of resistors connected in series is equal to the sum of the individual resistances.
Mathematical Explanation
- From Kirchoff’s second law, the total p.d. is equal to the sum of the p.d.s across each resistor: V = V1 + V2 +…
- Because V = IR, this can be rewritten as IR = IR1 + IR2 +…
- From Kirchhoff’s first law, the current through each resistor is the same so I is a constant.
Giving R = R1 + R2 +…
Derive and explain the relationship between resistors connected in parallel.
Describe how complex circuit problems can be solved.
EXAM NOTE: When tackling any complex circuit problem, we should start with Kirchhoff’s circuits laws and these four key electrical relationships.
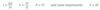
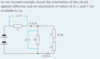
Describe and explain the loss of energy as a result of current in a power source.
- Whenever there is a current in a power source, work has to be done by the charges as they move through the power source. In a chemical cell, this work done is due to reactions between the chemicals. In a solar cell, it is due to the resistance of the materials of the cell.
- As a result, some energy is ‘lost’ (transferred to heat) when there is a current in the power source, and not all energy transferred to the charge is available for the circuit.
- The p.d. measured at the terminals of the power source (the terminal p.d.) is less than the actual e.m.f. We call this difference ‘lost volts’
Describe the relationship between the e.m.f, the terminal p.d. and the lost volts.
electromotive force = terminal p.d. + lost volts
Describe and explain the conditions under which the e.m.f changes.
- In normal use, the e.m.f does not change.
- However, changing the current can affect the lost volts and terminal p.d.
- Increasing the current means that more charges travel through the cell each second and so more work is done by the charges, increasing the lost volts. This lowers the terminal p.d.
Derive a relationship between e.m.f. and terminal p.d using the concept that
electromotive force = terminal p.d. + lost volts)
Describe how the internal resistance and e.m.f. of a cell can be found.
Describe how internal resistance can be very high or very low depending on the application.
Derive the potential divider equation.
- Describe how a varying Vout can be produced.
- How can a the Vout be made to vary with temperature?
- How can the Vout be made to vary with light intensity?
Describe the use of potentiometers rather than potential dividers to produce a varying Vout.
