Chapter 6: Materials

Question 1

1. What are tensile and compressive forces?
2. How is an object made to be extended or compressed?

Answer 1

1. Forces that produce the extension of an object are known as tensile forces, and those that compress an object are called compressive forces.
2. Extension and compression are caused by applying two equal and opposite forces on either end of an object.

Question 2

1. Describe tensile deformation and compressive deformation.
2. State Hooke’s law.
3. Describe the areas of elastic deformation and plastic defomration in the force-extension graph of a spring.

Answer 2

1. A helical spring undergoes tensile deformation when tensile forces are exerted and compressive deformation when compressive forces are exerted.
2. Hooke’s law states that the extension of a spring is directly proportional to the force applied. This is true as long as the elastic limit of the spring is not exceeded.
3. In the force-extension graph of a spring, there is a straight line from the origin up to the elastic limit of the spring. In this linear region (where Hooke’s law applies), the spring undergoes elastic deformation. This means that the spring will return to its original length when the force is removed.
   Beyond the elastic limit, the spring undergoes plastic deformation: permanent structural changes to the spring occur and it does not return to its original length when the force is removed.

Question 3

1. Explain the equation F=kx.
2. A spring with a large force constant is difficult to…

REMEMBER: The equation also applied to the compression of a spring. Hookes law can be applied to any material, such as wires under tension and concrete columns under compression.

Answer 3

1. For a spring obeying Hooke’s law, the applied force F is directly proportional to the extension x. Therefore F=kx, where k is named the force constant of the spring (SI units newtons per metre). This is a measure called the stiffness of a spring.
2. A spring with a large force constant is difficult to extend and would be referred to as a stiff spring.

Question 4

Describe the primary practical used to investigate Hooke’s law.

Answer 4

1. Attach a spring at one end using a clamp, boss and clamp stand secured to the bench using a G-clamp or large mass.
2. Set up a metre rule with a resolution of 1mm close to the spring.
3. Suspend slotted masses from the spring and , as eah one is added, record the total mass added and the new length of the spring.

The accuracy of length measurements can be improved by using a set square, and by taking readings at eye level to reduce parallax errors.
You might also measure the mass of each slotted mass using a digital balance.
To obtain reliable results, there should be at least six different readings which have each been reported at least once.

Question 5

1. Describe what happens to the work done when a material is compressed or extended without going beyond its elastic limit.
2. What if the material has gone through plastic deformation?
3. How is the work done on a spring found from a force-extension graph?
4. Describe the energy transfer involved when work is done on a spring before its elastic limit is reached.

Answer 5

1. When a material is compressed or extended, without going beyond its elastic limit, the work done on the material can be fully recovered.
2. If the material has gone through plastic deformation, then some of the work done on the material has gone into moving its atoms to new permanent positions. This energy is not recoverable.
3. The area under a force-extension graph is equal to the work done on the spring.
4. The work done on a spring before its elastic limit is transferred to elastic potential energy within the spring. This energy is fullu recoverable because of the elastic behaviour of the spring.

Question 6

1. The elastic potential energy for a spring is equal to…
   (Derive an equation for Hooke’s law.)
2. Derive the equation E=1/2kx².

Answer 6

1. The elastic potential energy for a spring is equal to the area under its force-extension graph, which is equal to the area of the triangle the force-extension graph forms under Hooke’s law. Hence E_k = 1/2Fx [where F is the force producing an extension x].
2. Image attached.

Question 7

Describe the loading and unloading graph for metal wire.

Answer 7

Question 8

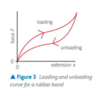
Describe the loading and unloading graph for rubber

Answer 8

• Rubber bands do not obey Hooke’s law. The rubber band will return to its original length after the force is removed – elastic deformation – but the loading and unloading graphs are both curved and are different.
• The ‘loop’ formed by the loading and unloading curves is called a hysteresis loop.
• As the area under the force-extension graph is equal to the work done, it can be concluded that more work is done when stretching the rubber band than is done when its extension decreases again.
  
  • Thermal energy is released when the material is loaded then unloaded.

Question 9

Describe the loading and unloading graph for polythene.

Answer 9

• A polythene strip does not obey Hooke’s law. Thin strips of polythene are very easy to stretch and they suffer plastic deformation under relatively little force.

Question 10

What is tensile stress?

Answer 10

Tensile stress is defined as the force applied per unit cross-sectional area of the wire. So

tensile stress = force / cross-sectional area [or σ = F / A]
where σ (Greek letter sigma) is the tensile stress in pascals, F is the applied force in newtons, and A is the cross-sectional area in m².

Question 11

What is tensile strain?

Answer 11

Tensile strain is defined as the fractional change in the original length of the wire. So

tensile strain = extension / original length [or ε = x / L]
where ε (Greek letter epsilon) is the tensile strain, x is the extension, and L is the original length.

Question 12

Why does tensile strain not have any units?

Answer 12

Tensile strain is the ratio of two lengths, so has no units. Tensile strain may also be written as a percentage.

Question 13

Describe and explain the stress-strain graph for a metal.

Answer 13

• This is a typical stress-straon graph for mild (low-carbon) steel, a ductile material. A ductile material can easily be drawn into a wire or hammered into thin sheets.
• Stress is directly proportional up to P, the limit of proportionality (the region in which Hooke’s law is obeyed).
• E represents the elastic limit: materials sometimes do not obey Hooke’s law up to this limit but elastic deformation still occurs up to this limit.
• Y1 and Y2 are the upper and lower yield points, where the material extends rapidly. This part of the curve is typical of mild steel but may be absent from other ductile materials.
• Point UTS represents the material’s ultimate tensile strength. This is the max stress that a material can withstand when being stretched before it breaks.
• Beyond this point, the material may become longer and thinner at its weakest point (necking).
• The material ultimatel snaps at the breaking point B.

Question 14

1. What is the breaking strength of a material?
2. What is a strong material?

Answer 14

1. The breaking strength of a mterial is the stress value at the point of fracture.
2. A strong material is one with a high ultimate tensile strength.

Question 15

What is the Young modulus? Explain.

Answer 15

Within the limit of proportionality, stress is directly proportional to strain. Hence, the ratio for a particular material is constant and is known as the Young modulus, E. That is

Young modulus = tensile stress / tensile strain [or E = σ/ε]
where the unit for the Young modulus is the same as that for stress, Nm^–2 or Pa.

Question 16

How is the Young modulus E of a material determined from a stress-strain graph?

Answer 16

The Young modulus E of a material is the gradient of the linear region of the stress-strain graph. It is not dependant on the shape or size of a material.

Question 17

How can the stiffness of materials be compared?

Answer 17

The stiffness of materials can be compared by comparing their Young modulus values. For example, a material with a large Young modulus is stiffer than one with a smaller Young modulus.

Question 18

How can the Young modulus of a material be experimentally determined? Describe and explain.

Answer 18

• The Young modulus of a material can be experimentally determined from a wire of that material with diameter d (measured using a micrometer) by applying various loads to it and measuring its length each time.
  
  • The setup: a wire of starting length greater than 1.00m is clamped securely at one end, passed over a pulley, and loaded with masses at the other end. The wire is marked with tape and a ruler is placed underneat to accurately determine the change in length.
• The cross-sectional area A of the wire can be calculated from πr² or (πd²)/4. The diameter d should be an average of several measurements taken from different places in the wire.
• The tensile force F acting on the wire can be calculated from the hanging mass m using F = mg.
• After applying each additional mass, the extension is calculated. There should be six different masses and at least one repetition.
• After plotting the stress-strain graph, the Young modulus of the material is determined (gradient of linear section of graph).

Question 19

Describe the stress-strain graphs for glass and cast iron.

Answer 19

• The stress-strain graphs for glass and cast iron, where the ultimate tensile strength is the same as the breaking strength, show that they are both brittle materials.
  
  • Brittle materials show elastic behaviour up to its breaking point, without plastic deformation.

Question 20

Describe the stress-strain graphs for polymeric materials.

Answer 20

Polymeric materials are materials that consist of long molecular chains. These behave differently depending on their molecular structure and temperature. For example, both rubber and polythene can stretch a lot before breaking, but rubber shows elastic behaviour while polythene shows plastic behaviour.