Chapter 8 Superposition Flashcards
(37 cards)
The Principle of Superposition
states that when two or more waves with the same frequency travelling in opposite directions overlap, the resultant displacement is the sum of displacements of each wave
-The principle of superposition applies to all types of waves i.e. transverse and longitudinal
The Principle of Superposition describes
how waves which meet at a point in space interact
When two waves with the same frequency and amplitude arrive at a point, they superpose either:
- in phase, causing constructive interference. The peaks and troughs line up on both waves. The resultant wave has double the amplitude or, in anti-phase, causing destructive interference.
- The peaks on one wave line up with the troughs of the other. The resultant wave has no amplitude
Stationary Waves
or standing waves, are produced by the superposition of two waves of the same frequency and amplitude travelling in opposite directions
-This is usually achieved by a travelling wave and its reflection. The superposition produces a wave pattern where the peaks and troughs do not move
—In order to produce a stationary wave, there must be a minima (node) at one end and a maxima (antinode) at the end with the loudspeaker

Stretched strings
-Vibrations caused by stationary waves on a stretched string produce sound
—This is how stringed instruments, such as guitars or violins, work
-This can be demonstrated by a length of string under tension fixed at one end and vibrations made by an oscillator:
—As the frequency of the oscillator changes, standing waves with different numbers of minima (nodes) and maxima (antinodes) form
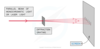
Microwaves
- A microwave source is placed in line with a reflecting plate and a small detector between the two
- The reflector can be moved to and from the source to vary the stationary wave pattern formed -By moving the detector, it can pick up the minima (nodes) and maxima (antinodes) of the stationary wave pattern

Air columns
-The formation of stationary waves inside an air column can be produced by sound waves
—This is how musical instruments, such as clarinets and organs, work
-This can be demonstrated by placing a fine powder inside the air column and a loudspeaker at the open end -At certain frequencies, the powder forms evenly spaced heaps along the tube, showing where there is zero disturbance as a result of the nodes of the stationary wave

A stationary wave is made up
nodes and antinodes -The nodes and antinodes do not move along the string. Nodes are fixed and antinodes only move in the vertical direction -Between nodes, all points on the stationary are in phase
nodes
are where there is no vibration
antinodes
are where the vibrations are at their maximum amplitude
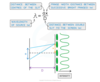
fundamental mode of vibration or the first harmonic
When a stationary wave, such as a vibrating string, is fixed at both ends, the simplest wave pattern is a single loop made up of two nodes and an antinode
- This is called the fundamental mode of vibration or the first harmonic
- The particular frequencies (i.e. resonant frequencies) of standing waves possible in the string depend on its length L and its speed v
–As you increase the frequency, the higher harmonics begin to appear
-The frequencies can be calculated from the string length and wave equation
Diagram showing the first three modes of vibration of a stretched string with corresponding frequencies

One or two open ends in air column

table showing all the different fundementials

Diffraction
is the spreading out of waves when they pass an obstruction —-This obstruction is typically a narrow slit (an aperture) -The extent of diffraction depends on the width of the gap compared with the wavelength of the waves —-Diffraction is the most prominent when the width of the slit is approximately equal to the wavelength
Diffraction is usually represented by a wavefront
as shown by the vertical lines in the diagram above -The only property of a wave that changes when its diffracted is its amplitude -This is because some energy is dissipated when a wave is diffracted through a gap
Interference
Interference occurs when waves overlap and their resultant displacement is the sum of the displacement of each wave This result is based on the principle of superposition and the resultant waves may be smaller or larger than either of the two individual waves
Interference of two waves can either be
-In phase, causing constructive interference. The peaks and troughs line up on both waves. The resultant wave has double the amplitude -In anti-phase, causing destructive interference. The peaks on one wave line up with the troughs of the other. The resultant wave has no amplitude
Waves are coherent if they have
the same frequency and constant phase difference
Coherence is vital
is vital in order to produce an observable interference pattern
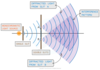
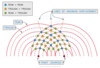
Demonstrating Two Source Interference: Using Water Waves
- Two-source interference in can be demonstrated in water using ripple tanks
- The diagram below shows diffracted circle shaped water waves from two point sources eg. dropping two pebbles near to each other in a pond
- The two waves interfere causing areas of constructive and destructive interference
- The lines of maximum displacement occur when all the peaks and troughs line up with those on another wave
Demonstrating Two Source Interference: Using Sound Waves
- Two source interference for sound waves looks very similar to water waves
- Sound waves are longitudinal waves so are made up compressions and rarefactions
- Constructive interference occurs when the compression and rarefactions line up and the sound appears louder -Destructive interference occurs when the compression lines up with a rarefaction and vice versa. The sound is quieter
—–This is the technology used in noise cancelling headphones

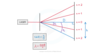
Demonstrating Two Source Interference: Using Microwaves
- Two source interference for microwaves can be detected with a moveable microwave detector
- Constructive interference: regions where the detector picks up a maximum amplitude
- Destructive interference: regions where the detector picks up no signal
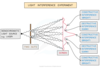
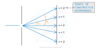
Demonstrating Two Source Interference: Using Light Waves
- For light rays, such as a laser light through two slits, an interference pattern forms on the screen
- Constructive interference is shown as bright fringes on the screen The highest intensity is in the middle
- Destructive interference is shown as the dark fringes on the screen These have zero intensity