Chapter 6 Deformation of Solids

Question 1

Tensile Force

Answer 1

When two forces stretch a body

Question 2

deformation

Answer 2

Forces don’t just change the motion of a body, but can change the size and shape of them too.

Question 3

compressive force

Answer 3

When two forces compress a body

Question 4

Tensile Strenght

Answer 4

Tensile strength is the amount of load or stress a material can handle until it stretches and breaks

Question 5

different materials beening stretched: steel, rubber and glass

Answer 5

Question 6

Hooke’s Law

Answer 6

-If a material responds to tensile forces in a way in which the extension produced is proportional to the applied force (load), we say it obeys Hooke’s Law

Question 7

limit of proportionality

Answer 7

is the point beyond which Hooke’s law is no longer true when stretching a material i.e. the extension is no longer proportional to the applied load

–The point is identified on the graph where the line is no longer straight and starts to curve (flattens out)

Question 8

A material obeys Hooke’s Law

Answer 8

if its extension is directly proportional to the applied force (load)

Question 9

Hookes law equation

Answer 9

F = kx

Question 10

k is the spring constant

Answer 10

of the spring and is a measure of the stiffness of a spring

• A stiffer spring will have a larger value of k
• It is defined as the force per unit extension up to the limit of proportionality (after which the material will not obey Hooke’s law)
• The SI unit for the spring constant is N m-1

Question 11

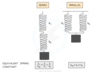
Spring constants for springs combined in series and parallel

Answer 11

Question 12

Stress (or tensile stress)

Answer 12

Tensile stress is the applied force per unit cross sectional area of a material

-The ultimate tensile stress is the maximum force per original cross-sectional area a wire is able to support until it breaks σ = F/A.

σ-stress(Pa) F=Force(N) A=Cross-sectional area (m^2)

Question 13

Strain

Answer 13

• Strain is the extension per unit length
• This is a deformation of a solid due to stress in the form of elongation or contraction
• Note that strain is a dimensionless unit because it’s the ratio of lengths ε = x/L ε-strain x-extension(m) L-length (m)

Question 14

how to find the cross-sectional area A

Answer 14

Question 15

Young’s Modulus

Answer 15

• The Young modulus is the measure of the ability of a material to withstand changes in length with an added load ie. how stiff a material is
• This gives information about the elasticity of a material
• The Young Modulus is defined as the ratio of stress and strain Young’s modulus = stress/strain = (FL0)/A(Ln − L0). -its unit is the same as stress: Pa (since strain is unitless)

Question 16

Young’s Modulus Experiment diagram look

Answer 16

Question 17

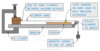
Method of determining young modulus experiment

Answer 17

1. Measure the original length of the wire using a metre ruler and mark this reference point with tape
2. Measure the diameter of the wire with micrometer screw gauge or digital calipers
3. Measure or record the mass or weight used for the extension e.g. 300 g
4. Record initial reading on the ruler where the reference point is
5. Add mass and record the new scale reading from the metre ruler
6. Record final reading from the new position of the reference point on the ruler
7. Add another mass and repeat method

Question 18

Young’s Modulus Experiment

Improving experiment and reducing uncertainties:

Answer 18

• Reduce uncertainty of the cross-sectional area by measuring the diameter d in several places along the wire and calculating an average
• Remove the load and check wire returns to original limit after each reading
• Take several readings with different loads and find average
• Use a Vernier scale to measure the extension of the wire

Question 19

Elastic deformation:

Answer 19

when the load is removed, the object will return to its original shape

Question 20

Plastic deformation:

Answer 20

when the load is removed, the object will not return to its original shape or length. This is beyond the elastic limit

Question 21

Elastic limit:

Answer 21

the point beyond which the object does not return to its original length when the load is removed

Question 22

Brittle and ductile materials

Answer 22

• Brittle materials have very little to no plastic region e.g. glass, concrete.
• The material breaks with little elastic and insignificant plastic deformation
• Ductile materials have a larger plastic region e.g. rubber, copper. The material stretches into a new shape before breaking

Question 23

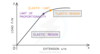
To identify these materials on a stress-strain or force-extension graph up to their breaking point

Answer 23

—A brittle material is represented by a straight line through the origins with no or negligible curved region —A ductile material is represented with a straight line through the origin then curving towards the x-axis

Question 24

Area under a Force-Extension Graph

Answer 24

-The work done in stretching a material is equal to the force multiplied by the distance moved -Therefore, the area under a force-extension graph is equal to the work done to stretch the material -The work done is also equal to the elastic potential energy stored in the material

Question 25

For the region where the material obeys Hooke’s law

Answer 25

the work done is the area of a right angled triangle under the graph

Question 26

For the region where the material doesn’t obey Hooke’s law

Answer 26

the area is the full region under the graph. To calculate this area, split the graph into separate segments and add up the individual areas of each

Question 27

Elastic Potential Energy

Answer 27

-Elastic potential energy is defined as the energy stored within a material (e.g. in a spring) when it is stretched or compressed -It can be found from the area under the force-extension graph for a material deformed within its limit of proportionality

Question 28

Calculating Elastic Potential Energy

Answer 28

Hooke's Law: F= kx EPE = 1/2Fx = 1/2(kx)x -Elastic potential energy can be derived from Hooke’s law Elastic potential energy = 1/2 kx^2

Question 29

Extension

Answer 29

Distance moved by a force Represented by x or e

Question 30

Materials and their tensile strength (Mpa) -concrete -rubber -human skin -glass -human hair -steel -diamond

Answer 30

-concrete 2-5 -rubber 16 -human skin 20 -glass 33 -human hair 200 -steel 840 -diamond 2800