Chapter 8 Flashcards
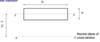
What are the sections that can be taken from a symmetrical beam?
Top Fibre: AB
Middle Fibre: GH
Bottom Fibre: CD
Random fibre: EF
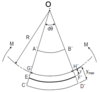
What happens to the top and bottom sections after a bending moment has been applied to the beam?
Top fibre: AB ⇒ A’B’
Bottom fibre: CD ⇒ C’D’
What happens to the middle sections are a bending moment for a symmetrical beam?
The length of the middle fibre remains the same but curves
How is the angle of bend calculated?
GH=G’H’ = Rdθ
GH/R = dθ
For the random fibre, how is the strain of this fibre calculated using the change in the fibre length?
εx = (E’F’ - EF)/EF
For the random fibre, how is the strain calculated from the angle of bend and lengths R and y? What is the chain of equations?
εx = (E’F’ - G’H’)/EF
εx = ((R+y)dθ - Rdθ)/Rdθ
εx = ydθ/Rdθ
εx = y/R
How is R an indication of strain?
εx = 1/R
Large R means a small strain
Small R means a large strain
Whats the equation for youngs modulus law?
E = σ/ε
How can be stress of a fibre be related to the lengths R and y?
σx/E = y/R
σx = Ey/R
What is the stress past the neutral plane and what is the trend?
Tension and increases linearly with distance from the neutral plane.
σx = Ey/R
E = Constant
R = Constant
What is the stress before the neutral plane and what is the trend?
Compression and decreases linearly with distance up to the neutral plane.
σx = Ey/R
E = Constant
R = Constant
What is the method to determine the centroid position for a non-uniform object
- A reference plane is determined
- The cross section is split into sections with a regular area which can be calculated
- Measure the distance from the reference plane to the centre of the regular areas.
- Use the equation
What is the equation to determine the centroid position for a non-uniform object?
y = ∑yiAi / ∑Ai
For sub section i:
yi = centre of subsection
Ai = Area of subsection
Prove that the centroid of a cross-section must be the neutral axis?
σ = dF/dA
∑F = 0
∫ dF = 0
∫ σdA = ∫ Ey/R dA = 0
(E/R) ∫ ydA = 0
E/R ≠ 0
so ∫ ydA = 0
y = 0
Therefor the centroid of a cross-section must be the neutral axis
How is the bending moment calculated?
∑M = 0
∑Fy = 0
∫ y σ dA + M = 0
M = ∫ y σ dA
M = (E/R) ∫ y^2 dA
How is the second moment of inertia calculated?
I = ∫xx (∫yy y2 dy)dx
e.g. Rectangle section
I = ∫b/2-b/2 (∫h/2-h/2 y2 dy)dx
I = ∫b/2-b/2 [(1/3)y3] dx
I = ∫b/2-b/2 [(1/3)(h/2)3-(1/3)(-h/2)3] dx
I = ∫b/2-b/2 [(1/12)h3] dx
I = [(1/12)h3] × ∫b/2-b/2 dx
I = [(1/12)h3] × [x]b/2-b/2
I = [(1/12)h3] × [(b/2) + (b/2)]
I = bh3/12
What is the second moment of area for a rectangular section?
Izz = (bh^3)/12
b = Base
h = Height
What is the second moment of area for a circular sections?
I = (πR^4)/4
R = Radius
What is the second moment of area for a semicircular section?
I = 0.110R^4
R = Radius
What is the second moment of area for a circular tube?
A = 2πR[m]t
R[m] = Radius from the centre to the middle of the tube section thickness
t = Thickness
This equation is only valid for t = R/10
What is the second moment of area for a half circular tube?
I = 0.095π((R[m])^3)t
What is the second moment of area for a triangular section?
I = (bh^3)/36
How is the bending moment calculated with the distance R and the youngs modulus?
M = EI/R
What is the bending relationship equations?
M / I = σ / y = E / R
How can stress be calculated from the second moment of inertia?
σ = My/I
How can the second moment of area be calculated when it is translated away from the neutral axis but is parallel?
Izz = Iz’z’ + A(y[=])^2
Izz = (bh^3)/12 + bh(y[=])^2
For a non uniform cross-section, how is the second moment of area calculated?
The non-uniform shape is broken up into different uniform sections and then the second moment of areas are added together.
Izz1 = Iz’z’1 + Ay[=2]^2
Izz2 = Iz’z’2+ Ay[=2]^2
I = Izz1 + Izz2
