Chapter 7 - Crystals Flashcards
(32 cards)

Hexagonal Close Packing
Hexagonal Close Packing
Atoms: 2
Lattice points: (0,0,0), (1/3, 2/3, 1/2)
Dimensions: 2r, 2r, 2.83r
Angle of 120º in parallelogram base

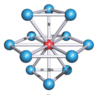
Cubic Close Packing
Cubic Close Packing
Atoms: 4
Lattice-points: (0,0,0), (1/2, 1/2, 0), (0,1/2,1/2), (1/2, 0, 1/2)

What are the types of holes?

In a single layer, what are the different ways we can pack atoms?

How can we calculate the lengths of the sides/radius of the atom able to fit in the center of a unit cell?

Packing efficiency

Primitive Cubic Structure
Atoms: 1
Lattice points: (0,0,0)
Sides: 2r

Body centered cubic
Atoms: 2
Lattice Points: (0,0,0), (1/2,1/2,1/2)
Sides: 2.31r

For a close-packed structure, how many holes are there per atom?
Two tetrahedral holes + one octahedral hole per atom
Metallic crystals
Most metals crystallize in body-centered cubic, cubic close-packed, and hexagonal close-packed structure
Changes in pressure/temperature can change the structure of many metallic crystals
Bonding in metals is nondirectional (each atom is bonded to all neighboring atoms, rather than to individual atoms), so dislocations –> deformation is possible
Dislocations
imperfections in crystals where atoms are out of place, but persist due to crystal rigidity
What effect do dislocations have on metals?
Dislocations make the metal more susceptible to physical deformation
This effect is heightened by added impurity atoms (especially with a size different from that of the host). These foreign atoms tend to accumulate at crystal dislocations, making the crystal structure even less uniform.
Describe sodium chloride NaCl crystal structure
Face-centered cubes of sodium ions and face-centered cubes of chloride atoms, offset by half a unit cell length in one direction

Describe the Zinc Blende (ZnS) crystal structure
Zinc blende is one of the two common crystalline forms of ZnS. It is also the most common zinc ore and has the same geometry as diamond, with alternating layers of zinc and sulfide.
A face-centered lattice of sulfide ions with each zinc ion in a tetrahedral hole (4). Half of the total tetrahedral holes in the cell (4 atoms/unit cell x 2 tetrahedral holes/atom = 8 tetrahedral holes available) are occupied.

Describe the wurtzite form of ZnS
Wurtzite is one of the two common crystalline forms of ZnS. However, wurtzite is much rarer than zinc blende and is formed at higher temperatures.
The zinc and sulfide ions each occupy the tetrahedral holes of the other ion’s hexagonal close-packed lattice.
Half of the total tetrahedral holes in each lattice is occupied.
Per unit cell there are (1/8)x8 + 1 = 2 atoms per hexagonal packing unit cell. Thus, there are 4 available tetrahedral holes, 2 of which are occupied by the other ion.

Describe the fluorite (CaF2) crystal structure
Calcium ion in a cubic close-packed lattice, with eight fluoride ions surrounding each calcium ion and occupying all of the tetrahedral holes (face centered cubic = 4 atoms/unit cell, 4atoms x 2 tetrahedral holes/atom = 8 tetrahedral holes/unit cell)
Or, can also be thought of as the fluoride ions in a simple cubic array with calcium ions in alternate body centers.
Found in all the oxides and sulfides of Li, Na, K, and Rb, and in Li2Te and Be2C

What crystal structure can you expect for alkali halides (e.g. LiCl)?
Like the structure for NaCl. Face-centered cubic unit cells for each atom offset by half a unit cell.

What compound has a crystal structure with ions in face-centered lattices and the other ion in the tetrahedral holes of this lattice?
ZnS Zinc Blende and Diamond (except with the same atom instead of ions).
What compound has a crystal structure with a hexagonal unit cell and the other ion occupying half of the tetrahedral holes?
ZnS Wurtzite
Antifluorite structure
The cation-anion stoichometry of CaF2 is reversed. That is, for compounds like Li2Te, Be2C
Every tetrahedral hole in the anion lattice is occupied by a cation.
Common for structures with X2F stoichometry (for oxiodes and sulfides)
Born-Haber cycle
A cycl that considers the series of component reactions that can be imagined as “steps” for compound formation, to give the final heat of formation. It basically applies Hess’s law (which states that the overall change in energy of a process can be determined by breaking the process down into steps, then adding the changes in energy of each step) to an ionic solid.

What enthalpies are positive and what enthalpies are negative for the reactions in the Born Haber cycle?
Positive:
- Sublimation ( Na(s) —> Na(g) )
- Ionization ( Na(g) —> Na+(g) + e- )
- Bond dissociation ( 1/2 Cl2 (g) —> Cl (g) )
Negative:
- Electron affinity ( Cl (g) + e- —> Cl- (g) )
- Lattice enthalpy ( Na+ (g) + Cl- (g) —> NaCl (s) )
- Heat of formation ( Na (s) + 1/2 Cl2 (g) –> NaCl (s) )


