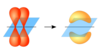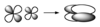Chapter 4 - Symmetry and Group Theory Flashcards
symmetry elements
mirror planes, axes of rotation, inversion centers, etc
symmetry opration
the actual reflection/rotation/inversion operation
Identity operation
E, no change in molecule
Rotation operation
Cn, rotation through 360º/n
Reflection operation
σ, reflection through mirror plane
Inversion operation
i, each point moves through the center of the molecule to a position opposite the original position and as far from the central point as where it started
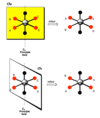
Rotation-reflection operation
Sn, aka improper rotation: rotation of 360º/n followed by reflection through a plane perpendicular to a axis of rotation
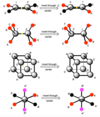
E
Identity operation, no change
Cn
Rotation operation, 360/nº each time
σ
Reflection operation through mirror plane
σh
Horizontal reflection operation when the plane is perpendicular to the principal axis of rotation
σv/σd
Vertical reflection operation when the plane contains the principal axis of rotation
σd: Dihedral passes through fewer atoms (dihedral to the angle of the bonds). Dihedral, same plane as v but related by half a rotation of the principle axis
σv: Vertical, parallel to/passing through the principal axis (primary rotation axis)
i
Inversion, each point moves through the center of the molecule to a position opposite the original position and as far from the central point as where it started
Sn
Rotation-reflection/improper-rotation operation, rotation of 360º/n followed by reflection through a plane perpendicular to a axis of rotation
Principal axis
The Cn axis with the largest value of n
Point group
a set of symmetry operations that best describes the molecule’s overall symmetry
Groups of low symmetry
C1 - no symmetry other than the identity operation
Cs - only one mirror plane
Ci - only an inversion center
Groups of high symmetry
C∞v - Linear molecule with an infinite number of rotations and an infinte number of reflection planes containing the rotation axis (e.g. H-Cl). Do not have a center of inversion.
D∞h - Linear molecule with an infinite number of rotations and an infinite number of reflection planes containing the rotation axis.
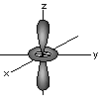
d orbital: z2
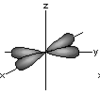
d orbital x2-y2
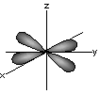
dxy
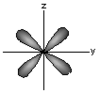
dyz
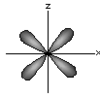
dxz
σ-bond
orbitals are symmetric to rotation about the line connecting the nuclei
no nodes that include the line between nuclei
π-bond
a change in sign in the wave function with C2 rotation about the bond axis
one node including the line between nuclei
δ-bond
change in sign on C4 rotation about the bond axis
two nodes including the line between nuclei
Identify rotation axes
What is the difference between dihedral and vertical mirror planes?
σd: Dihedral passes through fewer atoms (dihedral to the angle of the bonds). Dihedral, same plane as v but related by half a rotation of the principle axis
σv: Vertical, parallel to/passing through the principal axis (primary rotation axis)
