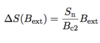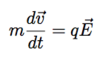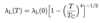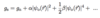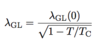Brainscape's Knowledge GenomeTM


Top Flashcards (Certified)
All Flashcards

Advanced Experimental Physics II > Chapter 4: Superconductivity > Flashcards

Chapter 4: Superconductivity Flashcards

(74 cards)

Start Studying
1
Q

Superconductivity

(Overview: 3 points)

A
  • Below critical temperature TC:
    • Perfect conductor: resistivity vanishes
    • Perfect diamagnet: repels magnet field inside with χ = −1
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

Superconductivity

(Types: 6 points)

A
  • Type-I (Conventional):
    • Can be described with BCS Theory
    • Can completely expel external field below Bcth
  • Type-II (Unconventional):
    • Cannot be described with BCS Theory
    • Have second critical field
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

Basic Properties

(Perfect Conductor: 2 points)

A
  • resistivity vanishes below TC
  • Drops within ∆T = T(R = 0.9Rn)−T(R = 0.1Rn) for normal resistivity Rn
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

Basic Properties

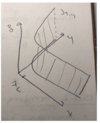
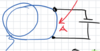
(Perfect Conductor [Measurement]: 3 points + diagram)

A
  • Measure current inductively by measuring induced magnetic field
    • B ∝ I
    • Lifetimes upto 1014 s have beeb measured
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

Basic Properties

(Perfect Diamagnet [Meissner Effect: Overview]: 2 point + diagram)

A

Can distinguish between perfect and superconductor by looking at response in magnetic field below TC​

  • Meissner Effect: ability of superonductor to expel magnetic fields below critical field Bcth when supercooled
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

Basic Properties

(Perfect Diamagnet [Meissner Effect: Supercooled with B = 0]: 4 points + diagram)

A
  • Same response when B-field switched on
    • Lenz Law → induced surface currents shield magnetic field
  • Same response when B-field switched off
    • No magnetic moment
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

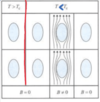
Basic Properties

(Perfect Diamagnet [Meissner Effect: Supercooled with B > 0]: 6 points)

A
  • Different response when supercooled
    • Perfect conductor: magnetic field penetrates
    • Superconductor: magnetic field expelled
  • Different response when B-field switched off
    • Perfect conductor: persistent magnetization becuase of Lenz currents
    • Superconductor: no magnetization
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

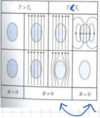
Basic Properties

(Critical Field [Overview]: 2 point + diagram)

A
  • Because Meissner effect is reversible → superconductivity can be destroyed by critical magnetic field Bcth
    • ​Otherwise, superconductor could do infinite work to push out magnetic field
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

Basic Properties

(Critical Field [Temperature Dependence])

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

Basic Properties

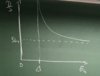
(Critical Field [Magnetization Inside]: 2 points + graph)

A
  • Bcth < 0 → can increase with extenral field
  • Bcth > 0 → magnetization breaks down
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

Basic Properties

(Critical Field [Field Inside]: 2 points + graph)

A
  • Bcth < 0 → external field shielded
  • Bcth > 0 → external field penetrates
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

Basic Properties

(Flux Quantization [Overview]: 2 points)

A
  • Experiments show that magnetic flux through a superconducting ring is an interger of a flux quantum (see below)
  • Experimental evidence of Cooper pairs
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

Basic Properties

(Flux Quantization [Experiment]: 1 point + graph)

A
  • Trap magnetic flux in supercooled lead tube and measure torque it causes on mirror
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

Thermodynamic Properties

(Overview: 3 points)

A
  • For type-I and -II superconductors in magnetic field, look at
    • Enthalpy
    • Entropy
    • Specific Heat
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

Thermodynamic Properties

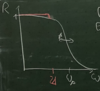
(Type-I [Enthalpy]: 3 points + graph)

A
  • Phase transition at B = Bcth
    • For B < Bcth → change in enthalpy ∆G ∝ B2 (Meissner parabola)
    • B >= Bcth → enthalpy is that or normal state (≈ contst.)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

Thermodynamic Properties

(Type-I [Enthalpy: Condensation Energy]: 3 points)

A
  • Difference between normal and superconducting enthalpy density at B = 0
    • ∆g = gn(0,T)−gs(0,T) = Bcth2/(2µo)
    • field repulsion energy needed to push external field out
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

Thermodynamic Properties

(Type-I [Entropy: Overview]: 2 points + graph)

A
  • Recall:
    • entropy of normal state Sn ∝ T
    • enthalpy of normal state gn ∝ T2
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

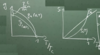
Thermodynamic Properties

(Type-I [Entropy: Take-Away]: 2points)

A
  • In B-field: first-order transition
  • No B-field: second-order transition
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

Thermodynamic Properties

(Type-I [Specific Heat: Overview]: 3 points)

A
  • Specific heat is measurable
  • Rutger’s formula gives different between normal and superconducting state ∆C = CN - CS
    • For T = TC → ∆C < 0
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

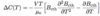
Thermodynamic Properties

(Type-I [Specific Heat: Take-Away]: 1 point + graph)

A
  • Heat capacity is greater in superconducting state
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

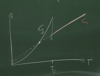
Thermodynamic Properties

(Type-I [Summary]: 3 points)

A
  • Enthalpy → condensation energy
  • Entropy → first-(second-)order phase transition with(out) B-field
  • Specific heat → superconducting state has higher heat capacity
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

Thermodynamic Properties

(Type-II [Overview]: 3 points)

A
  • There exist two critical field Bc1, Bc2
    • <em>​</em>B < Bc1 → same as type-I (Meissner effect)
    • B > Bc1 → external field is not fully repelled
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q

Thermodynamic Properties

(Type-II [Enthalpy]: 2 points + graph)

A
  • Bc1 < B < Bc2 → Shupnikov effect
    • enthalpy density increases slower than B2
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
Q

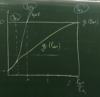
Thermodynamic Properties

(Type-II [Entropy])

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
25
Thermodynamic Properties | (Type-II [Specific Heat])
26
London Equations | (Overview: 3 points)
* Describe perfect conductor and perfect diamagneti with classical electrodynamics * Can account for Meissner effect * Can use to derive supercurrent carrier density *n*s
27
London Equations | (Assumptions: 4 points)
* EOM from Drude model with no scattering *τ*, *σ* → ∞ * charge carrier density *n*(*T*) = *n*n(*T* ) + *n*s(*T* ) consists of normal and supercarriers * *T* \< *T*C → *n*n = 0 and *n*s = *n* * *T* \> *T*C → *n*n = *n* and *n*s = 0
28
London Equations | (First Equation: 2 points)
Relates supercurrent density ***J***s = *n*s*q*s***v***s to external field *E*
29
London Equations | (Second Equation: 3 points)
* From Faraday's law of induction ∂t [∇ × (*Λ**J***s) + ***B***] = 0 * From Meissner effect, change in flux *and* static field have to induce screening
30
London Equations | (London Penetration Depth: 3 points)
* from field screening equation ∇ × ***B*** = *µ*o***J*** * _***​***London penetration depth_ *λ*L2 = *Λ*/*µ*o
31
London Equations | (London Penetration Depth [Temperature Dependence])
* Empirical relation
32
London Equations | (Take-Away [Overview]: 2 points)
* Consider superconducting material for *x* \>= 0 * There exist *B*-field penetration and supercurrent in superconducting material
33
London Equations | (Take-Away [B-field]: 1 point + 1 graph)
Permits exponentially decaying B-fields (e.g. type-II)
34
London Equations | (Take-Away [Supercurrent]: 1 point + 1 graph)
Supercurrent along surface
35
London Equations | (Take-Away [Notes]: 4 points)
* Thin films (∼ *λ*L) are not field free * Superconducitivity is DC phenomenon * For AC, normal carrier start to scatter * Can generalize London equations by assuming macroscopic wave function *ψ*(***r***,*t*) such that |*ψ*(***r***,*t*)|2 ≡ *n*s(***r***,*t*)
36
Ginzburg-Landau Theory | (Overview: 5 points)
* Describes spartial vartiation of *n*s by extending Landau's theory for second-order phase transition * Order parameter *g*s is complex and spatially varying * Distinguish between: * Spatially homogeneous with *B* = 0 * Spartially varying with *B* \> 0
37
Ginzburg-Landau Theory | (Spatially Homogeneous, *B* = 0 [Assumptions]: 4 points)
* |*ψ*(***r***,*t*)|2 = |*ψ*(***r***,0)|2 = |*ψ*o(***r***)|2 = constant * Expand *g*s in terms of |*ψ*o(***r***)|2 * ​*β* \> 0 otherwise large |*ψ*o(***r***)| → *g*s \< *g* * *α* must change sign at *T*C → *α*(*T*) = *α*\*(1 − *T* /*T*C)
38
Ginzburg-Landau Theory | (Spatially Homogeneous, B = 0 [Take-Away]: 5 points)
* Can relate the following to *α*, *β* * *​*supercurrent carrier density *n*s * condensation energy ∆*g* * ​Meaning of *α* * condesation energy for forming one Cooper pair
39
Ginzburg-Landau Theory | (Spatially Homogeneous, *B* = 0 [∆g vs |*ψ*o(***r***)|]: 3 points + graph)
* _Left_: above *T*C * _MIddle_: below *T*C * _Right_: complex |*ψ*o(***r***)|
40
Ginzburg-Landau Theory | (Spatially Varying, *B* \> 0 [Assumptions])
* Again, expand *g*s around |*ψ*o(***r***)|2, but include terms for field repulsion and spartial variance of order
41
Ginzburg-Landau Theory | (Spatially Varying, *B* \> 0 [Take-Away]: 2 points)
* Last term is measure of *stiffness* → large variation over short scale require lots of energy * Finding ground state *ψ*o(***r***) by minimizing ∆*g* leads to _First and Second GL Equations_
42
Ginzburg-Landau Theory | (Penetration Depth: 2points)
* *λ*GL = *λ*L/2
43
Ginzburg-Landau Theory | (Coherence Length: 2 points)
Local perturbations in density decay expoentially with this characterstic length
44
Ginzburg-Landau Theory | (Ginzburg-Landau Parameter: 3 points)
* *κ* \< 1 → type-I * *κ* \> 1 → type-II
45
Ginzburg-Landau Theory | (Spatial Ordering at Interface: 2 points + graph)
* No external field * No diffusion of carriers
46
Microscopic Description | (Goal)
Microscopic description of superconducting electron
47
Microscopic Theory | (BCS Theory [Overview]: 5 points + equation)
* There exists attractive interaction that forms Cooper pair * bosonic interation mediated by exchange boson * exchange of "virtual phonon" * Look for when Coulomb potential in medium with Thomas-Fermi screening is negative * _screened plasma frequency_ *Ω*p
48
Microscopic Theory | (BCS Theory [Take-Away]: 5 points + diagram)
* Consider energy difference between two electrons ∆E = Ek,1 − Ek,2 * for ∆*E*/(hbar) = *ω* \< *Ω*p → *V*C(*q*,*ω*) \< 0 * Pairing happens in k-space → retarded dynamics interaction * describes how attractive potential can arise * allows electrons to be far apart, otherwise Coulomb repulsion would dominate
49
Micoscopic Theory | (BCS Theory [Interaction Diagram])
50
BCS Theory | (Cooper Pairs [Assumptions]: 3 points)
* Free electron gas * *T* = 0 * all states up to *E*F are filled
51
BCS Theory | (Cooper Pairs [Overview]: 5 points + diagram)
* Add two electrons that interact via lattice by exchange of virtual phonon *q*D * Attraction maximized for ∆*k* = 0 → ***k***1 = −***k***2 * ​_Cooper pair_ * ​Describe with sum over all two-particle wavefunctions * |*A*k|2 ≡ probably of finding pair in state (***k***, −***k***)
52
BCS Theory | (Cooper Pairs [Take-Away]: 2 points + equation)
* Difference in energy of paired electrons ∆*E* makes Fermi sea unstable * Drives system to new phase → _BCS groundstate_
53
BCS Theory | (BCS Groundstate: 3 points + graph)
* Cooper pairs are bosons → can condense into macroscopic groundstate * Gap opens up at *E*F ± *∆* * *​*Even at *T*=0, there exist free states below *E*F → allows for continuous breaking of Cooper pairs
54
BCS Theory | (BCS Groundstate [Condensation Energy])
55
BCS Theory | (BCS Groundstate [Density of States]: 3 points + graph)
* Divergent for *E*k = ∆ * *E*k \>\> ∆ → DOS of free electron gas * Cooper pairs are *δ*-function at *E*k = 0
56
BCS Theory | (BCS State for *T* \> 0: 4 points + graph)
* As *T* → *T*C then ∆ → 0 * Thermal breaking of Cooper pairs and exitation of quasi-particles * Hinders exchange of virtual phonons * Can show ∆(0) = 1.764*k*B*T*C
57
Measuring ∆ | (Indirectly: 4 points + 2 graphs)
* Can measure indirectly by looking at specific heat * Heating superconductor → breaking of Cooper pairs and excitation of quasi-particles * Use Boltzmann statistics for population of excited quasi-particles * Specific heat *C* ∝ exp[−∆/(*k*B*T*)] only, since Cooper pairs do not contribute (_zero-entropic state_)
58
Measuring ∆ | (Directly: 2 points)
* Tunneling spectroscopy * Absorption spectroscopy
59
Measuring ∆ | (Optical Properties [Reflectivity]: 2 points + graph)
* Reflectivity jumps from metal curve to *R* = 1 for *ω* ∝ 2∆ * No absorption for *ω* \< 2∆ → total reflectivity
60
Measuring ∆ | (Optical Properties [Spectral Weight]: 2 points + 2 graphs)
* Spectral weight of *σ*1 jumps to *δ*-peak at *ω* = 0 after opening of gap * Induvtive response in *σ*2 → _Meissner effect_
61
Measuring ∆ | (Tunneling Spectroscopy [Setup]: 1 point + 1 diagram)
* Two thin conducting regions separated by small insulating region
62
Measuring ∆ | (Tunneling Microscopy [Main Idea]: 3 points + graph)
* Look at SC-Ins-NC junction * With correct bias |*eU*| ≥ ∆ electrons from SC can tunnel to quasi-particle states in NC * Allows for measurement of energy gap via current measurement
63
Josephson Junction | (Overview: 4 points + diagram)
* Sc-Ins-Sc with very thin insulating gap * Macroscopic wavefunctions in each side reach over into the other side * Phase difference between each wavefunction (hbar)(*φ*˙2−*φ*˙1) = −(*E*2− *E*1) = 2*eU* * Look at cases *U* = 0 and |*U* | \> 0
64
Josephson Junction | (Case *U* = 0: 3 points + graph)
* Constant phase difference drives current *I*s = *I*J sin(*φ*2 − *φ*1) * _DC-Josephson effect_: DC-current *I*s goes through insulator without voltage drop * Source delivers charges
65
Josephson Junction | (Case |*U* | \> 0: 2 points + graph)
* Quasi-particles begin tunneling * _AC-Josephson effect_: Current jumps from _Josephson current_ *I*J to finite value
66
Josephson Junction | (*B* \> 0: 2 points + diagram)
* Use pair of Josephson junctions → _SQUID_ * Allows precise magnetic flux measurements
67
Unconventional Superconductors | (Overview: 6 points)
* Virtual phonon is not only possible exchange boson * Could be slowing decaying spin fluctuation or _paramagnon_ * Different ways to define "unconventonal" * Electron-phonon interaction (yes/no) * Mean pair potential is (not) zero [conventional/unconventional * order parameter is same (lower) than underlying lattice symmetry [conventional/unconventional]
68
Unconventional Superconductors | (Completing Order Classification: 3 points)
* Effective interaction requires strong polarizability (structurally, electrically, etc.) → close to (structurally, electrically, etc.) instability → close to phase transition * Can tune mediating interaction by external control parameter (doping, pressure, etc.) * If tuning can result make order parameter zero → system is _quantum critical_ and fluctuations near _quantum critical point_ are important
69
Cuprates | (Structure: 2 points + 2 diagrams)
* Think of as stacks of Josephson junctions * _Apex oxygen_ strongly controls *T*C
70
Cuprates | (Electronic Structure: 5 points + 2 graphs)
* _Expectation_: chemical potential *µ* in middle of anti-bonding band → should be metal * _Reality_: experimentally shown to be good insulator * _Explanation_: * Strong crystal field splits anti-bonding level into upper-/lower Hubbard bands * *µ* now in gap * Similar to Mott insulator
71
Cuprates | (Electronic Structure [Doping]: 3 points)
* Doping by replacing L3+ → C4+ * ​Adds extra electrion to CuO layer, even though that's not where dopant goes * _Intrinsic modulation doped system_
72
Cuprates | (Fermi Surface: graph)
73
Cuprates | (Spin Structure and Phase Diagram: 3 points + diagram)
* t \<\< U → no hopping * Uncertainty principle → virtual hopping * Spin fluctuations are possible "glue"
74
Cuprates | (Superconducting Properties)
Highly anisotropic due to layers

Advanced Experimental Physics II (3 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2025 Bold Learning Solutions. Terms and Conditions