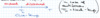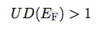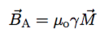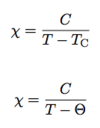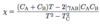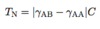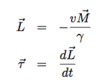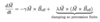Chapter 3: Magnetic Properties Flashcards
Magnetic Properties
(Overview: 5 points)
- Consider interation between solid and magnetic field
- Linear response regime
- Distinguish between quasi-bound and free electrons
- Quasi-Bound: magnetic properties are that of lattice atom
- Free: magnetic properties described by Fermi statistics
Macroscopic Quantities
(Assumptions)
- Consider insulting solid (i.e. no shielding currents) exposed to magnetic field
Macroscopic Quantities
(Magnetization and Magnetic Susceptibility: 2 points)
- External field leads to magnetization M
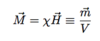
Macroscopic Quanities
(Magnetic Moment: 2 points)
- Classically given as (see below)
- When current due to single electron, I = -e/T with T = 2πr /v
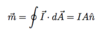
Macroscopic Quantities
(Magnetic Moment [Bohr Magneton]: 2 points)
- Consider Bohn quantization of orbital momentum L = movr ≡ (\hbar) → Bohr magneton
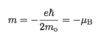
Macroscopic Quantities
(Magnetic Moment [For Solid])
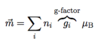
Macroscopic Quantities
(Magnetic Permeability)
Macroscopic Quantities
(Local Magnetic Field Hloc: 4 points)
- Similar as for local electric field
- Demagnetization field HN = -NM
- Lorentz field HL = M /3
- HL very small in para-/diamagnetic material because χ << 1
Macroscopic Quantities
(Demagnetization and Stray Field [Consider]: 2 points)
- Thin disk of ferromagnetic material
- Homogenous mangetization along normal of disk N = 1
Macroscopic Quantities
(Demagnetization and Stray Field [Take-Away]: 4 points and diagram)
- M induces B
- Inside disk: demagnetization field HN = B /µo - M
- Outside disk: stray field Hs = B /µo
- Amperes law only holds if Hs and HN in opposite directions
Macroscopic Quantity
(Magnetostatic Self-Energy: 4 points)
- Magnetostatic self-energy Em arises between each atomic magnetic moment interacts with the magnetic field create by all other moments in solid
- Energy of one magnetic moment µ in Hloc is Eµ = -µoµHloc
- Integrate over entire volume to get total self-energy (see below)
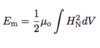
Microscopic Theory of Magnetic Properties
(Diamagnetic Solids: 2 points)
- Hext = 0 → no magnetic moments
- Hext > 0 → finite magnetization from induced magnetic moment opposite to applied field M = χdiH for χdi < 0
Microscopic Theory of Magnetic Properties
(Diamagnetic Solids [Types]: 6 points)
- Two types
-
Larmor Diamagnetism:
- atomic diamagnetism in insulator
- magnetic moments due to atoms or tightly bound electrons
-
Landau Diamagnetism:
- Magnetization of free electrons in metals
-
Larmor Diamagnetism:
Microscopic Theory of Magnetic Properties
(Paramagnetic Solids: 3 points)
- Magnetic moments even for Hext = 0
- Due to orbital electron motion µL or spin of crystal electrons µS
- Hext > 0 → magnetic moments align with external field M = χpaH with χpa > 0
Microscopic Theory of Magnetic Properties
(Russel-Saunders Coupling: 2 points)
- Orbital momenta couple to total orbital momenum L = ∑ili and spin couple to total spin S = ∑isi
- Total angular momentum given by Russel-Saunders Coupling J = L + S
Microscopic Theory of Magnetic Properties
(Paramagnetic Solids [Types]: 4 points)
-
Langevin Paramagnetism:
- due to atomic paramagnetism in insulators
-
Pauli Paramagnetism:
- due to conducting electrons in metals
Microscopic Theory of Magnetic Properties
(Ferromagnetic Materials: 5 points)
- For T < Tc → spontaneous magnetization without external field
- Results from exchange interaction causing spatial ordering of permanent magnetic moments
- Exchange interactions purely quantum mechanical:
- Pauli Principle
- Coulomb interaction
Microscopic Theory of Magnetic Properties
(Langevin Paramagnetism: 4 points)
- Classical description (good for large J)
- Look at thermodynamic value of magnetization M = nV<µz>
- For high Bext → <µz> = µ
- Saturation magnetization Ms = nVµ
Microscopic Theory of Magnetic Properties
(Langevin Paramagnetism [Curie Law])
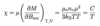
Microscopic Theory of Magnetic Properties
(Langevin Paramagnetism: diagram)
Microscopic Theory of Magnetic Properties
(Langevin Paramagnetism [QM Curie Law]: 2 points)
- two-level system
- similar description as classical Cure Law (up to factor 1/3)
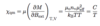
Para-/Diamagnetism of Metal
(Overview: 3 points)
- Recall: Effect of B-field on free electrons → Landau Diamagnetism
- Add contribution from electron spin → Pauli Paramagnetism
Para-/Diamagnetism of Metal
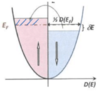
(Pauli Paramagnetism [Overview]: 2 points)
- Electron spin magnetic µs moment can take two values µs = ±µB
- Magnetization M = (n+ − n-)µB is function of spin-up/-down densities
Para-/Diamagnetism of Metal
(Pauli Paramagnetism [Curie Law]: 6 points)
-
Expectation:
- Curie-Law M = C /T
-
Reality:
- Curie Constant is no longer constant C = C(T)
-
Explanation:
- Only electrons near EF can respond to field, and this population increases with T
Para-/Diamagnetism of Metal
(Pauli Paramagnetism [More Details]: 3 points + diagram)
- Electron spins respond to Bext (see diagram)
- In thermal equilibrium, chemical potential must be equal → uncompensated spins flip
- Pauli spin susceptibility χP = const.
Para-/Diamagnetism of Metal
(Landau Diamagnetism [Overview]: 2 points)
- To get orbital contribution to magnetization, look at M ∝ ∂F/∂B
- Recall: Energy of electron depends on Bext (i.e. energy of Landau levels)
Para-/Diamagnetism of Metal
(Landau Diamagnetism [Take-Away])
- Landau diamagnetic susceptibility
- χL = −1/3χP(m/m* )2
Para-/Diamagnetism of Metal
(Total Susceptibility: 2 points)
χ = χL + χP
- χL and χP same order of magnitude → metals can be para- or diamagnetic
Cooperative Magnetism
(Overview: 4 points)
- Some materials have spontaneous polarization below characteristic frequency
- Caused by cooperative magnetism
- Finite interactions betewen atomic magnetic moments cause alignment
- Per usual, must distinguish between bound and free electrons
Cooperative Magnetism
(Dipole-Dipole Interaction: 2 points)
- max Edd (≈ 0.1 meV) << kT (≈ 25 meV)
- Dipole-dipole interaction too weak to explain ordering behavior at room temp
Exchange Interaction btwn Localized Electrons
(Exchange Constant: 8 points)
- Energy different between symmetric state (aligned spins) Es and anti-symetric state (opposite spins) Ea gives exchange constant JA = Es - Ea
- Sign determines type of ordering
- JA > 0 → ferromagnetic
- JA < 0 → anti-ferromagnetic
- Can also analyze via potential V(r1, r2) = Vion(r1) + Vion(r2) + Vee(r1, r2)
- Vee(r1, r2) > 0 → favors ferromagnetic behavior
- Vion(r1, r2) < 0 → facors anti-ferromagnetic behavior
- Material behavior depends on which dominates
Exchange Interactions btwn Localized Electrons
(Hubbard Model: 4 points)
- Simple model to describe hopping exchange of electrons
- Hamiltonian consists of two terms
- Hopping: hopping intergral t
- Repulasion: potential energy U
Exchange Interactions btwn Localized Electrons
(Types of Exchange: 7 points + diagram)
-
Direct Exchange:
- Overlapping orbits (e.g. covalent bonds)
-
Super Exchange:
- Indirect change via diamagnetic atom (e.g. via O2+ in MnO)
- Considered virtual hopping
-
Double Exchange:
- Combined hopping of electrons
Exchange Interaction of Free Electron Gas
(Take-Away)
There exists an exchange hold around free electrons that casues local density to drop in vicinity of free electron
Magnetic Order
(Types: 3 points)
- Ferromagnetism
- Ferrimagnetism
- Anti-ferromagnetism
Magnetic Order
(Stoner Model [Overview]: 5 points + diagram)
- Simplest model for understanding ferromagnetism in metals
- Exchange interaction facors parallel spin alignment
- Some electrons spontaneous redistribute from spin-down to spin-up
- To be spontaneous, redistribution must be energetically favorable
- i.e. decrease in potential energy must overcompensate increase in kinetic energy
Magnetic Order
(Stoner Model [Take-Away]: 3 points)
- Requiring ∆E < 0 → Stoner Criterion
- __When met, spin redistribution is energetically favorable
- Requires high correlation energy U and density of states at EF
Magnetic Order
(Ferromagnetism [Overview]: 5 points)
- T < TC → ferromagnetic
- T > TC → paragmangetic (thermal fluctuations disturb order)
- Second-order phase transition
- Magnetization M discontinuous
- Mangetic susceptibility χ continuous
Magnetic Order
(Ferromagnetism [Mean-FIeld Theory]: 6 points)
- Reduce magnetic moment interaction many-body problem to one-body problem by using effective field BA to account for exchange interaction
- Mean-field constant γ
- Virtual field
- Causes spatial order
- Measuring C, TC allows measurement of γ = TC/C
- Allows measurement of BA >> lab generated fields
Magnetic Order
(Ferromagnetism [Paramagnetic Regime]: 4 points)
- Susceptibility expectation vs reality (see below)
- Curie-Weiss Law
- Θ > TC
- Θ is measure of echange between paramagnetic momens not accounted for in mean-field theory
Magnetic Order
(Ferromagnetism [Susceptibility]: diagram)
Magnetic Order
(Ferrimagnetism [Overview]: 2 points)
- Anti-parallel spins, but not all spins are compensated → spontaneous magnetization
- Exchange constant JAB domiantes → anti-parallel only between A, B sites
Magnetic Order
(Ferrimagnetism [Susceptibility]: 5 points)
- Use near-field approximation
- Two Curie temperatures CA, CB<em> </em>and mean-field constants γAA = γBB = 0
- Critical temperature TC = |γAB|(CACB)1/2
- Susceptibility χ = µo∂(MA + MB)/∂Bext
Magnetic Order
(Ferrimagnetism[Susceptibility]: graph)
Magnetic Order
(Anti-Ferromagnetism [Motivation]: 3 points)
- MnO exhibits new Bragg peaks at low temperature in neutron scattering experiments → suggests double for unit cell
- X-ray scattering shows no new peaks → structure stays the same
- Suggests anti-ferromagnetic order for T < TN
Magnetic Order
(Anti-Ferromagnetism [Neel Temperature]: 5 points)
- Use same near-field appraoch as ferrimagnetism with:
- CA = C<span>B</span> = C
- γAA = γBB < 0
- MA = -MB
- Neel ordering temperature given by
Magnetic Order
(Anti-Ferromagnetism [Paramagnetic Regime]: 2 points)
- T > TN → susceptibility (see below)
- Curie-Weiss Temperature Θ = −|γAB + γAA|
Magnetic Order
(Anti-ferromagnetism [AFM Regime]: 5 points + diagram)
- Consider B perpendicular and parallel to spins
- Perpendicular: χ⊥ = |γAB|-1
-
Parallel:
- χ||(T=0) = 0
- Increasies toward χ||(T=TN) = χ⊥
Magnetic Order
(Susceptibility [Summary]: diagram)
Magnetic Anisotropy
(Overview)
Experiments show preferred direction of magnetization along easy axis and rejects mangetization along hard axis
Magnetic Anisotropy
(Anisotropy Energy: 8 points)
- Energy required to turn from easy- to hard-axis (see below)
-
Magneto-crystalline:
- Due to spin-orbital coupling
- Causes tilted spins
- Due to spin-orbital coupling
-
Shape:
- From demanetization tensor N being highly dependent on shape
-
Induced:
- Elastic tension and exchange anisotropy at interfaces
-
Magneto-crystalline:
Magnetic Domains
(Exp vs Reality: 3 points)
-
Expectation:
- For T << TC → M = MS
-
Reality:
-
M << MS because of domains
- M<span>domain </span>= MS
-
M << MS because of domains
Magnetic Domains
(Imaging: 2 points)
-
Magnetic Force Microscopy:
- Sharp magnetic tip scans magnetic material and responds to magnetic structure of sample
-
X-Ray Dichroism:
- Compare x-ray absorption spectrum to left- and rightcircularly polarized light
Magnetic Domains
(Stray Fields: 4 points + diagram)
- Magnetic domains reduce stray fields (see below)
- Edge domains minimize stray fields (right-most below)
- Magnetic field energy decreases
- Anisotropy and domain wall energy increases
Magnetic Domains
(Wall Types: 4 points + diagram)
-
Bloch Wall:
- Magnetization rotates out of the plane of the domain wall
-
Neel Wall:
- Magnetization rotates in the plane of the domain wall
Magnetization Curve
(3 points + diagram)
- Energy density ∝ area of hysteresis loop
- Beginning of dashed initial-line → reversible domain wall movement
- End of dashed initial-line → irreversible domain wall movement
Magnetization Dynamics
(Goal)
Determine how mangetization responds to external field
Magnetization Dynamics
(Assumptions: 2 points)
- Rigid spin coupling → homogeneous mode q = 0 (λ = ∞)
-
Equilibrium:
- Magnetization points along Beff
Magnetization Dynamics
(Out of Equilibrium: 3 points + 2 equations)
- Push magnetization out of equilibrium → system now feels torque τ = vM × Beff → precession of M around Beff
- Can relate angular momentum L to magnetic moment and torque (see below)
- gyromagnetic ratio γ = gµB/(hbar)
Magnetization Dynamics
(Take-Away)
Landau-Lipschitz equation
Ferromagnetic Resonance
(Overview: 2 points + diagram)
- If Bext oscillates at resonance frequency ωo = γBeff → leads to absorption
- No damping, because resonance condition met M x dtM = -MB1cosθ
Ferromagnetic Resonance
(Spectroscopy: 2 points + plot)
- Measure miscrowave absorption of thin film as function of DC field (see below)
- Can measure gyromagnetic ratio, anisotropy field, damping constant, …
Spin Waves
(Overview: 3 points)
- Recall: So far, considered spin-flip to be minimum excitation (q = 0)
- Now, consider colletive motion of spins with q > 0 → spin-waves emerge
- Angle between spins no longer zero → echange field BA becomes relevant
Spin Waves
(Magnon)
Spin waves are quantized quasi-particles
Spin Waves
(Different Modes: 2 points)
- Exchange Mode: small λ → BA domaintes Beff
- Dipolar Mode: large λ → BAni dominates at some point
Spin Waves
(Exchange Modes [Dispersion]: 5 points + 2 equations)
- Case: B = 0 and qa << 1
- Depends on (anti-)ferromagnetism (see below)
- Measure with neutron scattering spectroscopy or Raman spectroscopy
- Decay by Stoner excitations
- Single electron excitations
Spin Waves
(Exchange Mode [DIspersion]: graph)
How to measure magnetic susceptibility χ
(2 points + 2 diagrams)
- Faraday’s (left) Guoy’s Scale (right)
- SQUID
