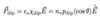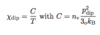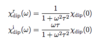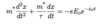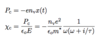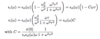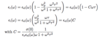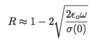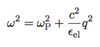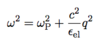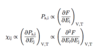Chapter 2: Dielectric Properties Flashcards
Goal of Studying Dielectrics Properties
(3 points)
Determine relation between microscoptic and macroscopic descriptions of how solids as a whole respond to electric field
- Microscopic VIew: photon creates phonon and/or electron-hole
- Macroscopic View: absorption described by Maxwell’s Equations and optical absoroption coefficient
Macroscopic Electrodynamics
(Assumptions: 2 points)
- Linear response
- i.e. small fields, no saturation effects, etc
Response of solid to electric field
(3 points)
- Depends on charge mobility
- Metals: free charge carriers → screening of E at short distances
- Insulators: small electron motion (polarization) → screening of E at long distances
Insulator response to
E = E*exp[i(qr-ωt)]
Small displacement induces polarization
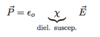
Dielectric Displacement Field
(2 points)
- Accounts for effects of free and bound charges in material (only free charges are source)
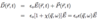
Dielectric Function
(Insulators: 3 points)
- Usually, wavelength of EM wave λ >> a lattice constant
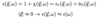
Metal response to
E = E*exp[i(qr-ωt)]
Electric current forms
Maxwell’s Equations
Generalized conductivity
(5 points)
- Consider ∇ × H with J = σE and D(ω) = εoε(ω)E
- Real part: due to free charges; dominates in metals
- Imaginary part: due to polarized charges
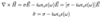
Generalized dielectric constant
(3 points)
- Real part: due to polarization
- Imaginary part: due to free charges
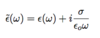
Kramer-Kronig Relationship
(Assumptions: 2 parts)
- Linear response
- E(ω) ∝ P(ω) → χ(ω) and ε(ω) are linear functions
Kramer-Kronig Relationship
(Take-Away)
- Measuring either real or imaginary part over entire sepctrum allows recovering the other part
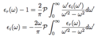
Absorption, Transmission, and Reflection of EM Radiation
(Overview)
There exists connection between dielectric properties and optical parameter of solid
Absorption, Transmission, and Reflection of EM Radiation
(Assumptions: 3 points)
- Uncharged solid ∇ · D = ρfree = 0
- Non-magnetic material µ = 0
- From MW-equations (see below)
- Should by vph2 in denominator
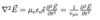
Absoroption, Transmission, and Reflection of EM Radiation
(Propagation (phase) Velocity)
Speed of EM wave in material
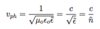
Absorption, Transmission, and Reflection of EM Radiation
(Complex Refractive Index: 2 points)
- n(ω): refractice index
- K(ω): absorption coefficient
Absorption, Transmission, and Reflection of EM Radiation
(Complex Wave Vector)
- Recall: Dispersion relation ω = ck/n
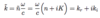
Absorption, Transmission, and Reflection of EM Radiation
(Complex refractive index: graph)
Absorption, Transmission, and Reflection of EM Radiation
(Take-Away)
- Solution with complex wave vector is damped wave (see below)
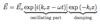
Absorption, Transmission, and Reflection of EM Radiation
(Take-Away: graph)
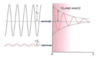
Absorption, Transmission, and Reflection of EM Radiation
(Take-Away: Absorption Coefficient)
Provides relationship between experimentall measureable quantity K and dielectric property of material ε
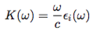
The Local Electric Field Eloc
Due to shielding, local electric field generally not identical to external field
The Local Electric Field
(The Dipole Electric Field Edip: 5 points)
- Lorentz field EL
- Depolarization field EN
- Depolarization factor N
- Macroscopic polarization P
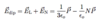
The Local Electric Field
(Diagram)
Microscopic Theory of ε(ω)
(Overview: 4 points)
- Solids classified based upon response to EM wave
- Dielectric
- Paraelectric
- Ferro-/Antiferroelectric
Dielectric Solids
(4 points)
- Can experience electronic or ionic polarization
- Typically dominate in insulators
- Both cases, restoring forces leads to forced harmonic oscillator with characterisitc eigenfrequency
- Metals are special case because no restoring force
Paraelectric Solids
(5 points)
- Solids with permanent electric dipoles
- Can experience orientation polarization
- Increases as temperature (external field) decreases (increases)
- Can experience orientation polarization
- Solid must have asymmetric molecules
- Characteristic frequencies small due to large mass
Ferro-/Antiferroelectric Solids
Experience spontaneous polarization
Electronic Polarization
(Overview: 4 points)
- Interaction of EM wave with solid leads to excitation of electron, i.e. it becomes polarized
- Intraband transitions
- Interband transitions
- Consider insulators, with only interband treansitions
Lorentz Oscillator Model
(Assumptions: 6 points)
- Ignore local electric field effects
- Negative electron bound to positive atomic core is perfect hamonic oscillator
- Excited by E(t ) = Eoe-<em>iωt</em> → forced, damped hamonic oscillator
- Equation of Motion (see below)
- Stationary solution x(t ) = (-e/m) f (ω) E(t )
- f (ω) is complex function
Lorentz Oscillator Model
(Atomic Polarizability: 2 points)
- Displacement x → dipole moment pel = −ex = εoαE
- Equating coefficients
Lorentz Oscillator Model
(Dielectric Function: 3 points)
- Look at connection between macro/micro descriptions
- P = εonvα(ω)E = εoχ(ω)E
- ε(ω) = 1 + χ(ω) = 1 + nvα(ω) = εr + iεi
Lorentz Oscillator Model
(Dielectric Function: graph)
Ionic Polarization
(Overview: 3 points)
- Caused by oppositely charged ions oscillating against eachother (i.e. optical phonons)
- Interaction of photon with ions of crystal ≡ collision between photon and optical phonon
- From conservation of moments |kphoton| ≈ 0 → only optical phonons with q = 0
Ionic Polarization
(Effect of Eloc [Overview]: 3 points)
- Additional force either strengthens or weakens restoring force
- Like electronic polarization, system is forced, damped harmonic oscillator
- Damping comes from heat dissipation
Ionic Polarization
(Effect of Eloc [Longitudinal Modes]: 3 points)
- Eloc is opposite relative ion displacement → enhanced restoring force
- Longitudinal eigenfrequency increases ωL > ωo
Ionic Polarization
(Effect of Eloc [Transverse Modes]: 2 points)
- Eloc is same direction as relative ion displacement → diminished restoring force
- Transverse eigenfrequency decreases ωT < ωo
Ionic Polarization
(Lyddane-Sachs-Teller Relation: 4 points)
- Only valid for q = 0
- ε(0) ≡ static value (ω ≈ 0) → photon in IR-range (ω << ωion,o )
- εstat ≡ value in visible range (ωion,o << ω << ωel,o )
Ionic Polarization
(Dielectric Function: graph)
Characteristic Eigenfrequencies
(2 points)
- Ions: IR region (1014 Hz)
- Electrons: UV region (1016 Hz)
Ionoic Polarization
(Forced Oscillaton: 3 points)
- Lattice vibrations induced by external field
- Photon: Transverse EM field → cannot excite longitudinal modes
- Electron: High energy → can excite longitudinal modes
Optical Properties of Crystal
(Dielectric Function: 3 points)
- Photons can only interact with phonons near center of BZ (i.e. intersection with optical branch)
- Consider only q = 0
Optical Properties of Crystals
(Dielectrifc Function Observations: 4 points)
- Singularity ω = ωT → total absorption by crystal
- Becomes zero at ω = ωL → agrees with longitudinal modes only possible for ε(ω) = 0
- For ωT < ω < ωL → ε(ω) < 0 → total relfection because index of refraction n = ε1/2 is imaginary
- For ωL < ω < ω<span>UV </span>→ ε(ω) > 0 → R < 1
Optical Properties of Crystals
(Polaritons: 3 points)
- For q > 0, apply results for ε(ω) to general dispersion ω2ε(ω) = c2q2
- Photon and phonon couple → polariton
- Difficult to excite
Optical Properties of Crystals
(Polariton Dispersion Relation: graph)
Orientation Polarization
(Static Polarization: 3 points)
- Paraelectric Materials have permanent dipoles
- Potential energy given by (see below)
- Only partial alignment PdipE << kBT
- Potential energy given by (see below)
Orientation Polarization
(Langevin-Debye Relation: 3 points)
- Relates Pdip to thermodynamic average of dipole (see below)
- One can show: <cos> = <em>p</em>dip<em>E</em>/(3<em>k</em>B<em></em>)
</cos><ul>
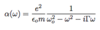
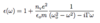
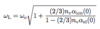
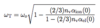
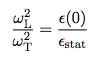
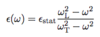
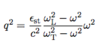
<li>Leads to Curie Law of MAgnetic Susceptability </li>
</ul></cos>
Orientation Polarization
(Curie Law of Magnetic Susceptibility)
Orientation Polarization
(Frequency Dependence: 3 points)
- Dipoles cannot follow arbitrarily high AC-fields → χdip(ω) decreases as ω increases
- Introduce relaxation time τ to account for dipole inertia (see below)
- Solutions: Pdip(t ) = Pdip(ω)[1 − exp(−t /τ)]
Orientation Polarization
(Debye Formula: 4 points)
- Assume χdip(ω) in Pdip(ω) = εoχdip(ω)E(ω) has real and imaginary part
- Solution has real and imaginary party (see below)
- Real part: dipole alignment
- Imaginary part: dielectric losses due to relaxation
Orientation Polarization
(Debye Formula: graph)
Full Dielectric Response of an Insulator
Dielectrics of Free Electron Gas
(Assumptions: 5 points)
- Free electron gas in AC-field (Drude model)
- Large wavelength q → 0
- EOM (see below)
- Solution
- x(t ) = -e/m* f(ω) E
Dielectrics of Free Electron Gas
(Polarization: 3 points)
Relative displacement of conducting electrons and ions leads to polarization (and restoring force)
Dielectrics of Free Electron Gas
(Dielectric Function: 3 points)
- Total dielectric function sum of bound electrons χel and conducting electrons χc
- Plasma frequency ωp2 ∝ nV
Dielectrics of Electron Gas
(Dielectric Function [Real/Imaginary])
Optical Properties of Metals
(Regimes: 3 points)
- Low-Frequency Regime
- Relaxation Regime
- Transparent Regime
Optical Properties of Metals
(Low-Frequency Regime: 3 points)
- ω << ωp → ωτ << 1 → C >> 1
-
εr = -εiωτ → εr << εi → lots of screening (i.e. losses much greater
- Near-perfect reflection (metals make good mirrors)
Optical Properties of Metals
(Low-Frequency Range [Hagen-Rubens Relation]: 2 points)
As σ(0) increases, R → 1
Optical Properties of Metals
(Low-Frequency Regime [Skin Depth]: 2 points)
More conductive → smaller skin depth, i.e. more screening
Optical Properties of Metals
(Relaxation Regime: 4 points)
- 1/τ < ω < ωp → electrons can follow, but scattering becomes important
- ωτ term dominates in denominator
- ε(ω) ≈ εr ≈ −εel(ω)ωp2/ω2
- Looking at complex index of refraction → K ≈ 1/ω
Optical Properties of Metals
(Transparent Regime: 4 points)
- ω >> ωp → ωp/ω << 1
- εr(ω) ≈ εel(ω) and εi(ω) ≈ 0 → ε(ω) ≈ εr(ω)
- Complex index of refraction ≈ 1
- Metals become transparent above ωp (UV range)
Optical Properties of Metal
(Dielectric Function: graph)
Longitudinal Plasma Oscillations
(Overview: 6 points)
-
Recall: Case for relflection → ε < 0
- Insulators: ω<span>L </span>< ω < ω<span>T</span>
- Metals: 0 < ω < ω<span>P</span>
- Suggests
- ωT = 0
- ωL = ωP
Longitudinal Plasma Oscillations
(Take-Away: 4 points)
- No transverse modes for electron gas
- Longitudinal restoring force is F = -eE
- Harmonic oscillator with plasma frequency ωP
- Collective longitudinal oscillation of conducting electrons is a plasmon
Longitudinal Plasma Oscillations
(Plasmon: 5 points)
Collective longitudinal excitation of conducting electrons
- Cannot be thermally or optically excited
- Excite using fast, charged particles
- Shoot through thin foil
- Energy loss of transmitted electorn is excitation energy of plasmon
Forced Transverse Plasma Oscillations
(Plasmon-Polariton [Overview]: 4 points)
-
Recall: General expression for dispersion of photons
- ω2 = c2q2/ε(ω)
- Consider relaxation regime
- Leads to plasmon-polariton
Forced Transverse Plasma Oscillation
(Plasmon-Polariton: 3 points)
- Transverse EM wave in metal
- Coupling of photon and phonon
Plasma Oscillations
(Plasmon Dispersion: graph + 2 points)
- Top: Bulk plasmon
- Bottom: Surface plasmon
Surface Plasmons
(Overview: 4 points + graph)
- Can be excited at interfaces between material with opposite signs of dielectric function
- Must use p-polarized light
- Only one wave in each half-space with exponentially decaying amplitude perpendicular to surface
- High concentration of electric field near surface
Surface Plasmon
(On Metal Surfaces: 5 points)
- εair = 1 and εmetal < 0 → surface plasmons
- Opticall excite with Kretschmann Configuration
- Detect dip in reflectivity when surface plasmon excited
- Very sensitive to change in delectric constant
- e.g. detect desorption process
Surface Plasmon
(On Metal Surfaces [Kretschmann Configuration]: diagram)
Excitons
(Expectation v. Reality: 2 points)
- Expectation: Interband transitions in semiconductor at low T for (h-bar)ω > Eg
- Reality: Excitation for (h-bar)ω < Eg → excitons
Excitons
(Properties: 4 points)
- Bound state between excited electron in conduction abnd and corresponding hole in valence band
- Absorption energy (h-bar)ω = Eg − Eexciton
- Can move through crystal as electron relaxes
- Bosons
Exictons
(Absoroption Profile: graph)
Excitons
(Frenkel Excitions: 2 points)
- Typical for material with strongly bounded electrons
- Smaller separation distance
Excitons
(Mott-Wannier Excitons: 2 points)
- Typical for matierals with weakly bonded electrons
- Spatial distance of electron-hole pair >> lattice spacing
Electron-Electron Interactions
(Static Screening: 2 points + figure)
- Place positive test charge into system
- Charges rearrange to create P- and D-fields, which cancel εE = (D - P ) = 0
Electron-Electron Interactions
(Thomas-Fermi Screening [Assumptions]: 4 points)
- Semi-classical theory
- Slowly varying potential with respect to Fermi length
- Constant chemical potential
- Low temperature
Electron-Electron Interactions
(Thomas-Fermi Screening [Take-Away]: 2 points)
-
ε(q ) = 1 + kf2/q2
- For q → 0, ε → ∞ and full screening for non-zero φext
Ferroelectricity
(Overview: 4 points)
- Materials with spontaneous polarization Ps that sets in below critical temperature, Curie temperature TC, without extenal field
- For T > TC → called paraelectric
- Can have either (anti-)ferroelectricity by switching external field
- Depends on structure
Ferroelectricity
(Pyroelectric)
Material where static field from spontaneous polarization is larger than switching field
Ferroelectricity
(Requirement for Ps: 2 points + diagram)
-
Polar axis: crystall cannot be roated 180 degrees into itself for any axis perpendicular to polar axis
- Existence does not guarantee ferroelectricity
Ferroelectricity
(Piezoelectric Material)
Material where spontaneous polarization sets in when squeezed
Ferroelectricity
(Order Parameter: 2 points)
- Phase transition defined according to an order parameter
- Here, spontaneous polarization Ps
Ferroelectricity
(Landau Theory [Overview]: 4 points)
- Examines free-energy density as function of spontaneous polarization to define phase transition
- Can relate spontaneous polarizability and susceptability to free energy F = U - TS
Ferroelectricity
(Landau Theory [Assumptions and Take-Away]: 2 points)
- Close to phase transition, Ps very small → expansion of free-energy density f(Ps, T, E ) around Ps (see below)
- For ferroelectric, a2 = γ(T − Tc) switches sign for finite To ≤ Tc
Ehrenfest Thermodynamic Classification Scheme for Phase Transitions
(First-Order)
First derivative of thermodynamic potential has discontinuity at phase transition
Ehrenfest Thermodynamic Classification Scheme for Phase Transitions
(nth-Order: 4 points)
nth-derivative of thermodynamic potential has discontinuity at finite value
- e.g. Second-order
- Ps = ∂F/∂E changes continuously
- χij = ∂2F/∂**E2 has discontinuity
Classification of Ferroelectrics
(5 points)
- Order-Disorder System
-
Displacive System
- e.g. Figure below
- If forces from local field > restoring forces → displacement occurs, i.e. freezing phonon
- Polarization Catastrophe: Polarization is classically infinite, but the displacement stops due to anharmonic effects
- e.g. Figure below
