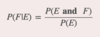Chapter 4: Probability, Randomness, and Uncertainty Flashcards
probability experiment (or trial)
any process with a result determined by chance
outcome
each individual result that is possible for a probability experiment
sample space
the set of all possible outcomes for a given probability experiment
event
a subset of outcomes from the sample space
tree diagram
- allows the outcomes to be organized in a systematic manner
- begins with the possible outcomes for the first stage and then branches for each additional possibility
- each of the elements of the last row in the tree diagram represents a unique outcome in the sample space
subjective probability
an educated guess regarding the chance that an event will occur
experimental (empirical) probability
- uses the outcomes obtained by repeatedly performing an experiment to calculate the probability
- rounding rule: when calculating probability, give the exact fraction or a decimal rounded to four decimal places; if extremely small, it is permissible to round the decimal to the first nonzero digit
Law of Large Numbers
the greater the number of trials, the closer the experimental probability will be to the true probability
classical (theoretical) probability
- the most precise type of probability
- can only be calculated when all possible outcomes in the sample space are known and equally likely to occur
properties of probability
(when an event includes the entire sample space, the probability is 1)
complement of an event E (Ec)
the set of all outcomes in the sample space that are not in E
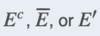
Complement Rule for Probability
P(E) + P(Ec) = 1
factorial
the product of all positive integers less than or equal to a given positive integer, n (0! = 1)
n! = n(n−1)(n−2) ⋯ (2)(1)
combination
a selection of objects from a group without regard to their arrangement
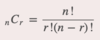
permutation
- a selection of objects from a group where the arrangement is specific (also when “repetitions are not allowed”)
- nPn = n!
special permutations
involve objects within a group that are identical
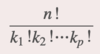
key terms
at least, at most, greater than, less than, between, etc.
and
multiply
or
add
Addition Rule for Probability
P(E or F) = P(E) + P(F) − P(E and F)
Addition Rule for Probability of Mutually Exclusive Events
when the events cannot happen at the same time:
P(E or F) = P(E) + P(F)
Multiplication Rule for Probability of Independent Events
when the outcome of one event does not influence the probability of the other:
P(E and F) = P(E) ⋅ P(F)
multistage experiment
- experiment with more than one step
- drawing one card from a deck vs. drawing a card, shuffling it back in, and drawing another
with or without replacement
- whether or not objects from the first stage of the experiment were placed back into consideration for a subsequent stage
- with replacement: creates independent events
P(E and F) = P(E) ⋅ P(F) - without replacement: creates dependent events
example: P(queen and then king) = 4/52 ⋅ 4/51
conditional probability, P(F | E)
- “the probability of F given E” for dependent events
- the probability of event F occurring given that event E occurs first
- answer is only the subsequent part of multistage experiment
Multiplication Rule for Probability of Dependent Events
when the probability of one is influenced by the probability of the first:
P(E and F) = P(E) ⋅ P(F | E)
OR
P(E and F) = P(F) ⋅ P(E | F)
Fundamental Counting Principle
- For a multistage experiment with n stages where the first stage has k1 outcomes, the second stage has k2 outcomes, and so forth, the total number of possible outcomes for the sequence of stages that make up the multistage experiment is k1 ⋅ k2 ⋅ k3 ⋅ … ⋅ kn.
- example: account “numbers” with two letters followed by three numbers
26 ⋅ 26 ⋅ 10 ⋅ 10 ⋅ 10 = 676,000
