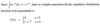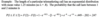Chapter 4

Question 1

Review: Continous Variable

Answer 1

• a rv X is continuous if possible values consist of an entire interval on the number line [possibly infinite in extent, e.g. (0, infinity))
• in general, a random variable is continuous if a measurement of some sort is required to determine its value
  
  • fuel efficiency (mpg), time necessary to complete a lap (min), commuting distance (miles)

Question 2

Probability Distribution of a Continous Random Variable

Answer 2

• specified by a mathematical function f(x), called the probability density function (pdf)
  
  • the graph of the pdf is called the density curve

Question 3

Density Curve

Answer 3

• graph of pdf
  
  • density curve cannot fall below horizontal axis, or else you would have negative probabilities
    
    • height of density curve above x = f(x) >= 0
  • total area under density curve = 1
    
    • f(x)dx = 1

Question 4

Let a and b be any two numbers with a

Answer 4

• the probability that the value of X falls someplace in the interval between a and b is the area under the density curve

Question 5

Example 4

The direction of an imperfection with respect to a reference line on a circular object such as a tire, brake rotor, or flywheel is, in general, subject to uncertainty.

Consider the reference line connecting the valve stem on a tire to the center point, and let X be the angle measured clockwise to the location of an imperfection. One possible pdf for X is

Answer 5

Question 6

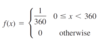
Example 4 (contd.)

Graph the pdf

Answer 6

Question 7

Example 4:

What is the probability that the angle is between 90º and 180º?

Answer 7

Question 8

What is the value of c?

Answer 8

Question 9

Continous Random Variables and Probability Distributions: Example

The probability that the machine in use for between 0.25 and 0.75 hours (between 15 minutes and 45 minutes) is:

Answer 9

Question 10

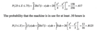
Continous Random Variables and Probability Distributions: Mean

Answer 10

Question 11

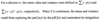
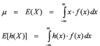
Continous Random Variables and Probability Distributions: Variance

Answer 11

Question 12

Continous Random Variables and Probability Distributions: Cumulative Distribution Function (cdf)

Answer 12

Question 13

Continous Random Variables and Probability Distributions: Cumulative Distribution Function (cdf)

Answer 13

Question 14

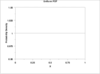
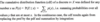
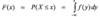
Continous Random Variables and Probability Distributions: Cumulative Distribution Function (cdf)

The cdf F(x)=P(X<=x):

The only possible values of X are numbers in the interval between 0 and 1, so

Answer 14

Question 15

Complete cdf of Example

Answer 15

Question 16

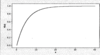
How to recapture pdf from cdf?

Answer 16

• By differentiation

Question 17

Finding the median of a continuous variable cdf:

Answer 17

• this is the value for which the area under the density curve to its left is 0.5, and the area under the density curve to the right of the value is also 0.5
• F(median) = 0.5
• Median is the 50th percentile of the distribution

Question 18

Expected Values, Variance, and Standard Deviation

Answer 18

Question 19

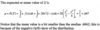
Expected Values, Variance, and Standard Deviation (contd.)

Answer 19

Question 20

Obtaining f(x) from F(x)

Answer 20

• For X discrete, the pmf is obtained from the cdf by taking the difference between two F(x) values. The continuous analog of a difference is a derivative.
• The following result is a consequence of the Fundamental Theorem of Calculus.

Proposition

• If X is a continuous rv with pdf f (x) and cdf F(x), then at every x at which the derivative F’(x) exists, F’(x) = f(x)

Question 21

Example - Uniform Distribution

Answer 21

Question 22

Example - Uniform Distribution (contd.)

Answer 22

• When X has a uniform distribution, F(x) is differentiable except at x = A and x = B, where the graph of F(x) has sharp corners.
• Since F(x) = 0 for x < A and F(x) = 1 for x > B, F’(x) = 0 = f(x) for such x.

For A < x < B,

Question 23

Specific Continuous Distributions: Uniform, Exponential, Normal

Answer 23

Question 24

PDF of Standard Uniform Distribution

Answer 24

Question 25

CDF of Standard Uniform Distribution

Answer 25

Question 26

Exponential Distribution

Answer 26

Question 27

Exponential Density Curves

Answer 27

Question 28

Exponential Distribution - Mean and Variance

Answer 28

Question 29

Exponential Distribution - Cumulative Distribution Function (cdf)

Answer 29

Question 30

Exponential Distribution - Plot of the cdf

Answer 30

Question 31

Exponential Distribution - Example

The length of a particular telemarketing call has an exponential distribution with mean value 1.25 minutes (lambda = 0.8). The probability that the call lasts between 1 and 2 minutes is:

Answer 31