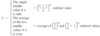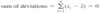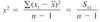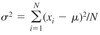Chapter 1 Flashcards
Population
The entire collection of individuals or objects about which information is desired
Census
When all of the desired information is avaiable for all objects or individuals in the population
Sample
A subset of the population because of limited time, resources, money, etc.
Types of Variables
1) Categorical 2) Quantitative or Numerical
Categorical Variable
A categorical variable places an individual or object into one of several groups or categories Ex) Gender, race, type-of-job, hair color
Quantitative or Numerical Variable
A Quantitative or Numerical Variable takes numerical values for which arithmetic operations such as adding and calculating an average value makes sense Ex) Age, salary
Discrete numerical data
Numerical data is discrete if it’s set of possible values are finite Ex) Your year in college (1, 2, 3 or 4)
Continous numerical data
Numerical data is continuous if it’s set of possible values form an entire interval on the number line Ex) Weight/height of an individual
Univariate Data
Observations made on a single variable for each object in the dataset Ex) The unemployment rate of each state (state = object and unemployment rate = single variable)
Multivariate Data
Observations made on multiple variables for each object in the dataset Ex) Each person -> age, gender, race, salary, job-type
Bivariate Data
Bivariate data is a special case of multivariate data, where observations are made on two variables for each object in the dataset
Branches of Statistics
Descriptive Statistics; Inferential Statistics; Probability
Descriptive Statistics
- Objective is to merely summarize and describe important features of the data that is collected - Graphical approach: stem-and-leaf plots, histograms, box-plots, pie-charts, scatter-plots etc. - Numerical approach: calculation of numerical summary measures such as arithmetic mean, median, mode, standard deviation, correlation coefficient etc.
Inferential Statistics
- Objective is to use information in the sample to make some sort of a conclusion (or inference) about the population from which the sample was selected - Includes Point-estimation, Hypothesis Testing, Confidence Interval Estimation, ANOVA, Linear Regression, etc.
Probability
- Forms a bridge between descriptive and inferential statistics - Probability makes assumptions about the structure of the population, and then asks questions about what might result from selecting a sample from the population (deductive reasoning)
Stem-Leaf Plot Construction
Separate each observation into a ‘stem” consisting of all but the final (rightmost) digit and a “leaf,” the final digit
Stem-Leaf Plot: Pros and Cons
Pros: - a quick way of describing and ordering data - generally easy to construct - displays the actual data values - easy way to obtain a general idea of the distribution of the data (e.g. symmetric, skewed, bimodal) - to be able to describe the data from a stem-and-leaf plot, look for: a typical or a representative value (e.g. median); extent of spread about the typical value; presence of any gaps in the data; number and location of peaks; outliers Cons: - not always easy to construct an appropriate stem
Relative Frequency
The proportion of times the value occurs in the sample For continuous data -> we have to create class-intervals and find the relative frequency for each class-interval
Construction of Histograms for Discrete Data
Area of each rectangle is proportional to the relative frequency of the value
Positive Skew of Histogram
A unimodal histogram with the right or upper tail stretched out more compared to the left or lower tail
Symmetric Histogram
Left half of the histogram is mirror image of right half
Unimodal Histogram
Histogram rises to a single peak and then declines
Bimodal Histogram
Histogram has two different peaks
Multimodal Histogram
A histogram with more than two peaks
Number of Peaks in a Histogram
The larger the number of class intervals, the more likely it is that bimodality or unimodality will manifest itself
Negative Skew of Histogram
A unimodal histogram with the left or lower tail stretched out more compared to the right or upper tail
Density Estimate
A smoothed histogram
Sample Size
- The number of observations in a sample
- Notation = n
- If two samples are simultaneously under consideration, either m and n; or n1 and n2
The Mean
- The most familiar and useful measure of the center is the mean, or arithmetic average of the set - The only point at which a fulcrum can be placed to balance the system of weights is the point corresponding to the value of x-bar.
- Notation: Sample Mean = x-bar
- Notation: Population Mean = µ
- µ = (sum of the N population values)/N
Deficiencies of The Mean
- Outlier can greatly affect the mean and make the mean an inappropriate measure of the center
Sample Median
- Obtained by first ordering the n observations from smallest to largest (with any repeated values included so that every sample observation appears in the ordered list)
Median Distribution
Quartiles
- Quartiles divide the data set into 4 equal parts, with the observations above the 3rd quartile constituting the upper quarter of the data set, the 2nd quartile being identical to the median, and the 1st quartile separating the lower quartile from the upper 3 quartiles
Percentiles
- Similarly, a data set (sample or population) can be even more finely divided using percentiles; the 99th percentile separates the highest 1% from the bottom 99%
Trimmed Mean
- a compromise between the sample mean and the sample median
- a 10% trimmed mean, for example, would be computed by eliminating the smallest 10% and the largest 10% of the sample and then averaging what remains
Range
- A measure of variability
- Computed by finding the difference between the largest and smallest sample values
- Defect = Range only depends on the two most extreme observations and disregards the positions of the remaining n-2 values
Deviations from The Mean
- A deviation will be positive if the observation is larger than the mean (to the right of the mean on the measurement axis) and negative if the observation is smaller than the mean
- If all the deviations are small in magnitude, then all xis are close to the mean and there is little variability.
- Alternatively, if some of the deviations are large in magnitude, then some xis lie far from the mean suggesting a greater amount of variability.
Sum of Deviations
- The average deviation is always zero
Sample Variance
- denoted by s2
Sample Standard Deviation
- denoted by s
- Note that s2 and s are both nonnegative. The unit for s is the same as the unit for each of the xis.
Population Variance
- Denoted by σ2
- For the population, the divisor is N and not N-1
- Note that σ2 involves squared deviations about the population mean µ.
- If we actually knew the value of µ, then we could define the sample variance as the average squared deviation of the sample xis about µ.
- However, the value of µ is almost never known, so the sum of squared deviations about x-bar must be used.
- But the xis tend to be closer to their average sample median than to the population average µ, so to compensate for this the divisor n – 1 is used rather than n
Population Standard Deviation
- Denoted by σ
Five Number Summary
- The five number summary consists of the smallest observation, the first quartile, the median, the third quartile, and the largest observation, written in order from smallest to largest
- Minimum
- Q1
- M
- Q3
- Maximum
To Calculate The Quartiles
- Arrange the observations in increasing order and locate the 50th percentile, or the median M in the ordered list of obsercations
- The 25th percentile, or the first quartile Q1 is the median of the observations whose position in the ordered list is to the left of the overall median
- The 75th percentile, or the third quartile Q3 is the median of the observations whose position in the ordered list is to the right of the overall median
Box-Plot
- A box-plot is a graph of the five number summary
- Box-plots are most useful for side-by-side comparison of several distributions
- Describes location and spread of a sample
- Procedure:
- Draw a rectangle with lower and upper edges at the 25th percentile, or 1st quartile, and the 75th percentile, or 3rd quartile
- Draw a horizontal line across the rectangle at the median
- Extend verticle lines, or whiskers, from the middle of the upper and lower edges of the rectangle to the minimum and maximum values
