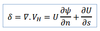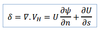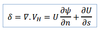Chapter 2: divergence and vorticity Part 2

Question 1

Convergence is defined as

Answer 1

the increase of mass within a given layer of the
atmosphere

Question 2

divergence is

Answer 2

the decrease of mass within a given layer of the atmosphere

Question 3

conditions for convergence to take place

Answer 3

the winds must result in a net inflow of, air into that layer

Question 4

For convergence to take place, the winds must result in a net inflow of, air into that layer. This type of convergence is generally associated with

Answer 4

low‐pressure area

Question 5

where convergence of winds toward the center of the low results in

Answer 5

an increase of mass into the low and an upward motion

Question 6

Divergence

Winds in this situation produce

Answer 6

a net flow of air outward from the layer

Question 7

Winds in this situation produce a net flow of air outward from the layer. We
associate this type of divergence with

Answer 7

high‐pressure cells

Question 8

Winds in this situation produce a net flow of air outward from the layer. We associate this type of divergence with high‐pressure cells, where the flow of air is directed

Answer 8

outward from the center, causing a downward motion

Question 9

The natural coordinate system describes

Answer 9

motion as normal or tangential to the radius of curvature of the flow

Question 10

how is the natural coordinate system represented

Answer 10

Rather than isobars,

flow is depicted as streamlines, which represent the instantaneous direction of the wind, and isotachs, the instantaneous wind speed

Question 11

We can construct natural coordinates with

Answer 11

unit vectors

Question 12

We can construct natural coordinates with unit vectors

Answer 12

n and , where

n is the normal vector and

s is the tangential vector

k is directed vertically upward

Ψ (angle) as the angle that the tangent of the curve makes with a fixed direction, and

the radius of curvature of the flow

Question 13

Note thatΨis defined as

Answer 13

positive in the counterclockwise direction and R > 0 for counterclockwise flow

Question 14

In the natural coordinate system the direction of the unit vectors is

Answer 14

not constant as in the Cartesian system

Question 15

In the natural coordinate system the direction of the unit vectors is not constant as in the Cartesian system, but is determined by

Answer 15

the direction of the wind

Question 16

In natural coordinate system, the horizontal divergence can be expressed as:

Answer 16

Question 17

explain the components

(the first term)

Answer 17

The first term, the directional divergence(convergence),represents the change in
angle with movement (or change in isobar spacing) across the flow.

Question 18

explain the components

(the first term)

The first term, thedirectional divergence(convergence),representsthechangein
angle with movement (or change in isobar spacing) across the flow. occures when

Answer 18

winds spreading outward (inward) at a constant speed, which represents a net
outflow (diffluence), or inflow (confluence)ofair.

Question 19

what is the condition of directional divergence and convergence

Answer 19

speed is constant in both cases

Question 20

show directional divergence and convergence

Answer 20

Question 21

the second term

Answer 21

thespeed divergence(convergence), occurs when downstream winds are faster (slower) than upstream winds for the same isobar spacing. More air is moving out (in) this area than moving in (out).

Question 22

condition of speed convergence and divergence

Answer 22

same isobar spacing

Question 23

show speed divergence and convergence

Answer 23

Question 24

According to the geostrophic relationship, which shows that

Answer 24

if the isobar spacing Δx remains constant, the wind speed doesn’t change

Question 25

Divergence of geostrophic winds equation and graph

Answer 25

Question 26

Also, if the isobar spacing becomes wider downstream (……………….), the wind
speed should

Answer 26

divergence

decrease (convergence)

Question 27

if the winds are purely geostrophic, the two terms

Answer 27

cancel each other out exactly and there will be no vertical motions.

Question 28

Thus, if the winds are purely geostrophic, the two terms cancel each other out exactly and there will be no vertical motions.
This shows that

Answer 28

the divergence of geostrophic winds is always zero, which can be proven mathematically also.

Question 29

Divergence of ageostrophic winds

where ………………………………… the winds are described as ageostrophic

Answer 29

there are vertical motions

Question 30

In areas, where there is ascent or descent, there is

Answer 30

mass being added to (or removed from) the airflow from some other level, which results in convergence (or divergence).

Question 31

examples for divergence of ageostrophic winds

Answer 31

1. speed convergence aloft
2. directional divergence aloft
3. Directional convergence and speed divergence

Question 32

Speed convergence aloft:

Answer 32

In this case, while Δx is constant, the speed is decreasing downstream.

Question 33

1. Speed convergence aloft: In this case, whileΔݔis constant, the speed is
   decreasing downstream. Thus, there is

Answer 33

an accumulation of mass aloft, and some of this excess mass is pushed down, resulting in divergence (and a high pressure system) at the surface directly below.

Question 34

show speed convergence aloft

Answer 34

Question 35

2. Directional divergence aloft:

Answer 35

In this case, whileΔx increases downstream,
the speed remains constant, which results in a low pressure system and
convergence at the surface.

Question 36

2. Directional divergence aloft: In this case, whileΔݔincreases downstream,
   the speed remains constant, which results in a low pressure system and
   convergence at the surface. Note that mass is being

Answer 36

added to the airflow from below due to rising motion. This explains why the winds are not slowing down even though the isobars are spreading out.

Question 37

show directional divergence aloft

Answer 37

Question 38

3. Directional convergence and speed divergence:

Answer 38

This is a case of geostrophic relationship, when Δx decreases downstream, the speed increases, which results in no raising or sinking motion and no mass is being added to or removed from the airflow.

Question 39

3. Directional convergence and speed divergence:This is a case of geostrophic relationship, when Δݔ decreases downstream, the speed increases, which results in no raising or sinking motion and no mass is being added to or removed from the airflow.

Therefore, these two terms

Answer 39

cancel each other and net convergence/divergence is zero. Neither divergence nor convergence occurs.