Chapter 2 Flashcards
What happened to the growth rate of per capita income after the industrial revolution?
Except for some bumps, per capita income growth has been close to 2% since 1900 in developed countries
What happened to differences between 1800 and 1950 in per capita income?
Increased in an extreme way as Western Europe, Australia, Canada, New Zealand and the US separated themselves from the rest of the world
What is the relationship between real per capita income and the rate of population growth?
Negatively correlated
What is the impact of higher female labour participation in developed countries?
means that they are having less kids and there is less of an incentive to have many kids as you would want to focus on one and the cost of childcare (E.g. University) is costly therefore costs would want to be saved
What were the conditions before the industrial revolution?
- No growth of any kind in any country
- GDP was constant
- Plauges and wars were common
What are the use of kids in developing countries?
maintain subsistence, as they are extra manpower and the cost of childcare is not high
What happened to the average hours worked in developed countries?
Tend to decreases
What tends to be growth rate for rich countries?
Around 2% and it tends to be alike unlike poor countries
What are the assumptions of the production model?
- Single, closed economy
- One consumption good
- No government
What are the three ways we can change Y?
- Capital stock changes
- Labour force changes
- Ability to produce goods with given resource changes
What does the production function show?
Shows how much output (Y) can be produced given any number of capital and labour
What are the inputs in the production process, as fixed amounts?
What is the production function?
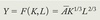
What does Y represent?
Output
What does this represent?
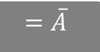
Productivity parameter
A lower level of TFP implies that workers produce less output for any given level of capital per person.
What represents the productivity parameter?
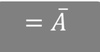
What does this represent?
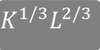
What does the bar on top of letters show?
It is constant
What are the inputs in the equations?
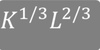
What does a higher value of the TFP mean?
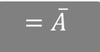
The higher the number, the greater amount of goods you are able to produce given capital and labour. Measure at how efficient the workforce in mixing capital and labour and therefore the overall efficiency of the production process. Differs with each countries. It includes regulations, institutions which make the production process possible and etc.
Why can we not explain why TFP changes overtime?
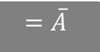
Assumed to be exogenous
What is the Cobb-Douglas Production Function?
What does α show?
Represents the GDP share of K & L
What is the returns to scale of the Cobb-Douglas Production Function?
Constant returns
- If K and L increase by x%, then Y also icreases by x%
- F(αK, αL) = αF(K,L) (Homogenous function, with a degree of 1)
- The addition of the powers on capital and labour add to one which signals to a constant return
What is the standard replication argument?
The addition of a firm with the same capital and labour, then the GDP doubles and adding one more firm leads to the GDP trippling from its original value
Summary
(Labour is fixed)
- Production function increases at a decreasing rate
- Gain from increasing capital falls as it runs into diminishing returns, due to the other constrained factor
Summary
- Marginal product of capital is the increase in quantity, as a result of adding one extra unit of capital
- Decreases, as we add more due to diminishing returns, as labour is constant
- When the capital stock is low, there is a huge effect which is why there is a huge gain
Summary
- Increase in labour means more is gained with the same amount of capital, as there are more people to handle the capital, therefore it is used more efficently
Summarise
- Increase in capital leads to an increase in MPL for the same labour input, as they have more capital to aid production, leading to greater efficency
What is the equation for GDP per capita and capital per person and definition?
Labour is constant
Assume everyone is working
y=f(k)=f(k,1)
What is used to denote per capita?
Lowercase letters
What is used to denote capital per worker?
Lowecase letter: k
Summarise:
GDP per capita
- F(k) is the cobb-douglas function y=F(k,1).
- It therefore gets all the properties of the production function like the slope which should be equal to the marginal product of capital
What is MPL?
- Increase in output, as a result of increasing labour input by 1 unit
- Derivative in terms of labour of production function
What is the marginal productivity of capital?
- Increase in output, as a result of increasing capital input by 1 unit
- Derivative in terms of capital of production function
In what instance would there be an increasing returns to scale?
When doubling inputs, output increases by more than double
In what instance would there be a decreasing return to scale?
When we double inputs, output increases by less than double
Summarise
Profits is the amount produced minus the cost of labour (cost of wages multiplied by the amount of workers) added with the cost of capital (cost of rental multiplied by the number of capital used by firm)
- π: profits
- r: rental rate of capital (Given under perfect market competiton)
- w: wage rate (Given under perfect market competiton)
- Hire capital until MPK (derivative of the profit function with respect to k) = r.
- Hire labor until MPL (derivative of the profit function with respect to l) = w
*Price of output is 1.
Adding each production together gives us GDP
- firms employ all the supplied capital and labor in the economy.
Summarise
2/3 of production is paid to labour
1/3 of production is paid to capital
Equal to the exponents on the inputs in the Cobb-Douglas function.
Summarise:
- 0 profits in the economy, which verifies the assumption about perfect competition
- Income = Production
- Assuming economic profit (the amount left over when total payments for inputs are subtracted from total revenue ) is equal to 0
What is the process of normalisation?
Setting the productivity parameter as 1
What is the issue of assuming the TFP=1?
- Poorer countries tend to be overstimated, as they have a much lower TFP, due to barriers, which negatively affect TFP.
What is TFP nicknamed?
Residual
Measure of ignorance
What is the definition of economic growth
Operational meaning: Long run increase in GDP (Everything is correlated to GDP)
General: Long-run improvements in general living standards (anything contributing to well being)
Why do we care about economic growth?
Growth rate makes huge contribution overtime
What is the rule of 70?
If GDP per capita grows at “g”% per year, then the number of years it takes y to double income is
70/g%
Only growth rate determines the amount of time taken
Small difference in growth rate lead to large differences over time
What is the constant growth rate rule?
What is the equation for computing a growth rate between year 0 and t?
What are the rules of growth rates?
Growth rates of ratios, products, and powers: Suppose two variables x and y have average annual growth rates of gx and gy, respectively. Then the following rules apply:
Then the following rules apply:
- If z = x/y, then gz = gx − gy.
- If z = x × y, then gz = gx + gy.
- If z = xa, then gz = a × gx.
In these expressions, gz is the average annual growth rate of z.
*Growth rate of GDP is the growth rate of GDP per capita plus the growth rate of the population
What are the costs of economic growth?
Environmental issues
Increased income inequality
Technological advances may also lead to the loss of certain jobs and industries
What is HDI
HDI tried to solve the unidimensional issue of GDP through including social factors
Includes health indicators and education indicators
Positively related to GDP per capita
What things are positively correlated to GDP per capita?
Hapiness
Pollution
What are the characterisitcs of countries with higher GDP per capita?
Low poverty
