Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

aqa a-level physics > Chapter 18 - Simple harmonic motion > Flashcards

Chapter 18 - Simple harmonic motion Flashcards

You may prefer our related Brainscape-certified flashcards:
Physics 101 flashcards AP® Physics flashcards
1
Q

What kind of motion will a pendulum perform?

A

Simple harmonic motion

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

Give some other examples of simple harmonic motion

A
  • child on swing
  • object on spring moving up and down repeatedly
  • ball-bearing rolling from side to side
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

What is equilibrium?

A

The centre point

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

What does an oscillating object do?

A

Moves repeatedly one way than in the opposite direction through its equilibrium position

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

What is the displacement of an object in SHM?

A

Direction and distance from equilibrium point

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

In one full cycle after being released from a non-equilibrium position, what does the displacement of an object do?

A
  • Decreases as it returns to equilibrium, then
  • reverses and increases as it moves away from equilibrium in the opposite direction, then
  • decreases as it returns to equilibrium, then
  • increases as it moves away from equilibrium towards it’s starting position.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

Define the amplitude of an object in SHM

A

Maximum displacement of oscillating object from the equilibrium position

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

When are oscillations described as free vibrations?

A

If the amplitude is constant and no frictional forces are present/ no external forces.

System oscillates at it’s natural frequency

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

What is the time period (T) of an object in SHM?

A

time for one cycle of oscillation

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

Define frequency for an object in SHM?

A

number of cycles per second made by an oscillating object.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

For 2 objects oscillating at the same frequency, what is the equation for their phase difference? (in radians)

A

phase difference = 2∏t/T

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

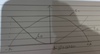
Draw the graph of displacement against time for an object in SHM

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

What does the gradient of the displacement-time graph show?

A

Velocity at the given time (velocity-time graph)
- v =d/t

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

Draw the graph of velocity against time for an object in SHM?

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

What does the gradient of the velocity-time graph show?

A

acceleration

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

Draw a graph of acceleration against time for an object in SHM?

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

Using the graphs, what is the relationship between acceleration and displacement?

A

acceleration is always in the opposite direction to the displacement

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

If the displacement-time graph is cos(x) what is the velocity-time and acceleration-time?

A

v-t - -sin(x)
a-t - -cos(x)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

What is the definition of SHM?

A

oscillating motion in which the acceleration is:

  1. ) proportional to the displacement, and
  2. ) always in the opposite direction to the displacement (towards equilibrium position)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

What is the equation definition of SHM?

A

a (directly proportional) -x

x = displacement

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

What is the definition of SHM including constant?

A

a = - (angular speed^2) x

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

What is the equation for displacement with respect to t?

A

x = A cos(angular speed x t)

A = amplitude

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q

What direction does the resultant force acting on the object in SHM act?

A

towards the equilibrium position (same as acceleration)

24
Q

What determines the frequency of oscillations of a loaded spring?

A
  1. ) Adding extra mass
  2. ) Using weaker springs
25
Q

Verify the equation T = 2∏ (m/k)^1/2

A
  • Assuming hooke’s law: T(s) = K x (change in) L
  • Change in tension acts as a restoring force when the object is oscillating. (change in) T(s) = -kx
  • a = restoring force/ mass = -kx/m
    a = -(angular speed^2) x
    where angular speed ^2 = k/m
    2∏f^2 = k/m
    f= 1/2∏ (k/m)^1/2
    T = 2∏ (k/m)^1/2
26
Q

Find angular speed^2 for simple pendulum

A
  • mgcos(angle) perpendicular to the path of the bob
  • mgsin(angle) along the path towards the equilibrium position.
  • restoring force, F=-mgsin(angle), a = F/m = -mg(angle)/m = -gsin(angle)
  • If (angle) is not over 10 degrees - sin(angle) = s/L where s = displacement from the lowest point. Therefore the acceleration, a = -g/L x s = - (angular speed^2) s where (angular speed^2) = g/L
27
Q

Prove T = 2∏ x L/g)

A

(angular speed^2) = g/L
(2∏f)^2 = g/L
f = 1/2∏ (g/L)^1/2
T = 2∏ (L/g)^1/2

28
Q

Describe the energy changes for a pendulum in SHM?

A

Energy changes from max kinetic at equilibrium position to max potential energy at max displacement points.

29
Q

Write the equation for potential energy

A 
Ep = 1/2 kx^2 
k = spring constant
30
Q

Write the equations for the total energy of system

A 
Et = 1/2 kA^2 
Et = Ek +Ep

A = amplitude

31
Q

Using Et = Ek + Ep, give an equation for Ek

A

Ek = 1/2k (A^2-x^2)

32
Q

Derive v = +- (angular speed) (A^2-x^2)^1/2 using Ek = 1/2k (A^2-x^2)

A

Ek = 1/2 mv^2, therefore: 1/2mv^2 = 1/2k(A^2-x^2)
(angular speed^2) = k/m, therefore v^2 = (angular speed^2) (A^2-x^2)
v = +-(angular speed) (A^2-x^2)^1/2

33
Q

What is the equation for maximum speed of SHM?

A

max speed = when x = 0

v^2 = (angular speed^2) (A^2-X^2) 
V = (angular speed) x A
34
Q

Draw the energy variation with displacement graph, with Ek, Ep and Et

A
35
Q

What conclusions can be made from the energy variation - displacement graph?

A
  • sum of the kinetic energy and potential energy is always equal to 1/2kA^2, which is Ep at max displacement. (same as Ek at 0 displacement).
  • 2 curves add together to get Et
36
Q

What does it mean when motion of SHM is damped?

A

Amplitude decreases over time due to friction and air resistance (dissipative forces) reducing total energy of system to e.g. thermal energy

37
Q

What is light damping?

A

occurs when the time period is independent of the amplitude so each cycle takes the same length of the time as the oscillations die away. Amplitude gradually decreases, reducing by the same fraction each cycle.

38
Q

What is critical damping?

A

Just enough damping to stop the system oscillating after it has been displaced from equilibrium and released. If damping is critical the oscillating system returns to equilibrium in the shortest possible time without overshooting.

39
Q

What is heavy damping?

A

occurs when damping is so strong that the displaced object returns to equilibrium much more slowly than if the system is critically damped. No oscillation motion

40
Q

What is a periodic force?

A

Force applied at regular intervals

41
Q

What is a system’s natural frequency?

A

System’s frequency when it oscillates without a periodic force being applied to it

42
Q

What are forced vibrations of a system?

A

When a periodic force causes a system to oscillate

43
Q

What is the frequency of the periodic force called?

A

applied frequency

44
Q

What happens as the applied frequency increases?

A
  • Amplitude of oscillations of the of the system increases until it reaches a maximum amplitude at a particular frequency, and then the amplitude decreases again
  • phase difference between displacement and the periodic force increases from 0 to 1/2∏ at the max amplitude then from 1/2∏ to ∏ as the frequency increases further.
45
Q

When is a system in resonance?

A

When the periodic force is in phase with the velocity

46
Q

What is resonant frequency?

A

frequency at maximum amplitude

47
Q

What effect does lighter damping have on amplitude at resonance and resonant frequency

A

Lighter the damping:

  • Larger max amplitude becomes at resonance
  • Closer resonant frequency is to the natural frequency of the system (resonance curve sharper)
48
Q

What happens as the applied frequency becomes increasingly larger than the resonant frequency?

A
  • Amplitude of oscillations decreases more and more
  • Phase difference between displacement and the periodic force increases from 1/2∏ until the displacement is ∏ radians out of phase with the periodic force.
49
Q

For an oscillating system with little or no damping at resonance, the applied frequency of the periodic force equals what?

A

natural frequency of the system

50
Q

What happens if a bridge is not fitted with dampers?

A

oscillate at resonance if subjected to suitable periodic force.

51
Q

What does the amplitude of oscillations depend on when a system oscillates at resonance with a costant amplitude?

A

Depends on amount of damping

52
Q

Which direction does a damping force acting on a vibrating system act?

A

Opposite direction to the velocity

53
Q

How does a bungee jumper show SHM?

A

After free fall, the bungee cord will have been extended to its full length and essentially acts as a spring, pulling the jumper back up, and hence the jumper will obey Hooke’s Law.

The jumper, being at the end of the bungee cord, will exert a downward gravitational force on cord and this downward force is balanced by the restoring force of the bungee cord, which is the upward force acting on the cord, in equilibrium.

This will result in the bungee jumper going up and down, oscillating about an equilibrium position, showing vertical SHM.

54
Q

How many peaks of potential energy are there in one oscillation of SHM?

A

2 peaks

55
Q
A
56
Q

A simple pendulum of time period 1.9s is set up alongisde another pendulum of time period 2s. The pendulums are displaced in the same direction and released at the same time. Calulcate the time interval they next move in phase.

A

difference of 1 oscillation, so Δt = 0.1 so n = 2 / 0.1 =20

20 oscillations of (shorter) pendulum and / or 19 oscillations of (longer) pendulum

ime to next in phase condition = 38 (s)

aqa a-level physics (31 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions