Chapter 1 Physical Quantities & Units Flashcards
The Newton (N), the unit of force, is defined by the equation
- Force = mass × acceleration
- N = kg × m s–2 = kg m s–2
- Therefore, the Newton (N) in SI base units is kg m s–2
The Joule (J), the unit of energy, is defined by the equation
- Energy = ½ × mass × velocity2
- J = kg × (m s–1)2 = kg m2 s–2
- Therefore, the Joule (J) in SI base units is kg m2 s–2
The Pascal (Pa), the unit of pressure, is defined by the equation:
- Pressure = force ÷ area
- Pa = N ÷ m2 = (kg m s–2) ÷ m2 = kg m–1 s–2
- Therefore, the Pascal (Pa) in SI base units is kg m–1 s–2
SI units table
Powers of Ten Table
Homogeneity of Physical Equations
- The units on either side of the equation should be the same
- to check the homogeneity of physical equations:
- Check the units on both sides of an equation
- Determine if they are equal
- If they do not match, the equation will need to be adjusted
A scalar
is a quantity which only has a magnitude (size)
A vector
is a quantity which has both a magnitude and a direction
Distance is a
scalar quantity because it describes how an object has travelled overall, but not the direction it has travelled in
Displacement is a
vector quantity because it describes how far an object is from where it started and in what direction
Scalars and Vectors Table
Condition for Equilibrium
- Coplanar forces can be represented by vector triangles
- In equilibrium, these are closed vector triangles. The vectors, when joined together, form a closed path
Resolving Vectors
- Two vectors can be represented by a single resultant vector that has the same effect
- A single resultant vector can be resolved and represented by two vectors, which in combination have the same effect as the original one
- When a single resultant vector is broken down into its parts, those parts are called components
For example, a force vector of magnitude F and an angle of θ to the horizontal is shown below
Random error
- Random errors cause unpredictable fluctuations in an instrument’s readings as a result of uncontrollable factors, such as environmental conditions
- This affects the precision of the measurements taken, causing a wider spread of results about the mean value
- To reduce random error: repeat measurements several times and calculate an average from them
Systematic error
- Systematic errors arise from the use of faulty instruments used or from flaws in the experimental method
- This type of error is repeated every time the instrument is used or the method is followed, which affects the accuracy of all readings obtained
- To reduce systematic errors: instruments should be recalibrated or the technique being used should be corrected or adjusted
Zero error
- This is a type of systematic error which occurs when an instrument gives a reading when the true reading is zero
- This introduces a fixed error into readings which must be accounted for when the results are recorded
Precision of a measurement:
- this is how close the measured values are to each other; if a measurement is repeated several times, then they can be described as precise when the values are very similar to, or the same as, each other
- The precision of a measurement is reflected in the values recorded – measurements to a greater number of decimal places are said to be more precise than those to a whole number
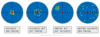
Accuracy:
this is how close a measured value is to the true value; the accuracy can be increased by repeating measurements and finding a mean average
The difference between precise and accurate results
These uncertainties can be represented in a number of ways:
- Absolute Uncertainty: where uncertainty is given as a fixed quantity
- Fractional Uncertainty: where uncertainty is given as a fraction of the measurement
- Percentage Uncertainty: where uncertainty is given as a percentage of the measurement
To find uncertainties in different situations:
-The uncertainty in a reading:
± half the smallest division
To find uncertainties in different situations:
-The uncertainty in a measurement:
at least ±1 smallest division
To find uncertainties in different situations:
-The uncertainty in repeated data
half the range i.e. ± ½ (largest – smallest value)
To find uncertainties in different situations:
-The uncertainty in digital readings:
± the last significant digit unless otherwise quoted
Combining Uncertainties (adding and subtracting)
- Adding / subtracting data – add the absolute uncertainties
- difference between measurements are added or subtracted as well as the ± uncertainties
Combining uncertainities: Multiplying / dividing data
add the percentage uncertainties
combining uncertainties: Raising to a power
- multiply the uncertainty by the power
