Chapter 1 Motion in a Circle Flashcards
(17 cards)
The angular displacement (θ) of a body in circular motion is defined as:
-The change in angle, in radians, of a body as it rotates around a circle
The angular displacement is the ratio of:
distance travelled around the circle/ radius of the circle
A radian (rad) is defined as:
The angle subtended at the centre of a circle by an arc equal in length to the radius of the circle
Angular displacement can be calculated using the equation:
Where:
Δθ = angular displacement, or angle of rotation (radians)
s = length of the arc, or the distance travelled around the circle (m)
r = radius of the circle (m)

Table of common degrees to radians conversions

The angular speed (⍵) of a body in circular motion is defined as:
- The rate of change in angular displacement with respect to time
- Angular speed is a scalar quantity, and is measured in rad s-1
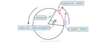
Calculating Angular Speed
-Taking the angular displacement of a complete cycle as 2π, the angular speed ⍵ can be calculated using the equation:
-W=ΔΘ/Δt = 2π/r = 2πf
- Where:
- Δθ = change in angular displacement (radians )
- Δt = time interval (s)
- T = the time period (s)
- f = frequency (Hz)
calculating angular speed at constant speed
- Angular velocity is the same as angular speed, but it is a vector quantity
- When an object travels at constant linear speed v in a circle of radius r, the angular velocity is equal to:
- ⍵=Δθ /Δt = v/r
- Where:
- v is the linear speed (m s-1)
- r is the radius of orbit (m)
This equation tells us:
- The greater the rotation angle θ in a given amount of time, the greater the angular velocity ⍵
- An object rotating further from the centre of the circle (larger r) moves with a smaller angular velocity (smaller ⍵)
What Causes Centripetal Acceleration?
- Velocity and acceleration are both vector quantities
- An object in uniform circular motion:
- is continuously changing direction, and therefore is constantly changing velocity
- The object must therefore be accelerating
- This is called the centripetal acceleration and is perpendicular to the direction of the linear speed
- Centripetal means it acts towards the centre of the circular path
Centripetal force and acceleration are always directed towards the centre of the circle diagram

‘tangential’ speed
The linear speed is sometimes referred to as the ‘tangential’ speed
Relating Centripetal Acceleration & Angular Speed
- An object travelling in uniform circular motion has centripetal acceleration, yet its angular speed (⍵) is constant
- This is because speed is a scalar quantity, whilst velocity is a vector quantity
- Therefore, angular speed is the magnitude (size) component of angular velocity
Key ideas to remember: when it comes to centripetal accelerton and anguar speed
- Angular speed (magnitude) stays constant, angular velocity (direction) is constantly changing
- Angular speed does not change with radius, but linear speed does
- The object’s centripetal acceleration is always directed toward the centre of the circle, and is perpendicular to the object’s velocity at any one time
- Velocity and acceleration are both defined by a change in direction, not just a change in the magnitude
Centripetal acceleration is defined as:
- The acceleration of an object towards the centre of a circle when an object is in motion (rotating) around a circle at a constant speed
- and can be defined by:
- a=v2/r
- v=r⍵
equations can be combined to give another form of the centripetal acceleration equation:
- a=v2/r
- v=r⍵
- combined equation is:
-
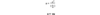
The centripetal force (F) is defined as:
- The resultant perpendicular force towards the centre of the circle required to keep a body in uniform circular motion
Centripetal force can be calculated using:
- Note: centripetal force and centripetal acceleration act in the same direction
- This is due to Newton’s Second Law
- The centripetal force is not a separate force of its own
- It can be any type of force, depending on the situation, which keeps an object moving in a circular path

Examples of centripetal force



