ch18

Question 1

Rutherford experiment disproved which model for the atom?

describe the model

Answer 1

The Thompson model or plum pudding model

atoms were a plum pudding with electrons embedded throughout a positive sphere

Question 2

how do you investigate the structure of an atom

Answer 2

with scattering experiments

particles are accelerated to a high energy and directed at a target

Question 3

Describe Rutherford’s experiment and his results

Answer 3

A stream of alpha particles from a radioactive source was fired at a very thin gold foil.

The angles at which the particles were scattered were recorded

some passed straight through (so most atom is empty space)

but a few of the alpha particles bounced right back from the foil being scattered at angles greater than 90 degrees

Question 4

What could Rutherford conclude after his experiment?

Answer 4

The atom is mainly empty space.

the core must be massive on an atomic scale to deflect alpha particles through large angles, but its much smaller than an atom as very few particles deflected through more than 90 degrees

alpha particles deflected due to electric repulsion between positively charged alpha particles and positive core in gold atoms.

The centre of the atom must have a large, positive charge. Rutherford named this the nucleus.

The nucleus must be tiny, but massive (mass).

Question 5

1 in how many alpha particles were turned back and what does this suggest about the size of a nucleus

diameter of atom

diameter of nucleus

Answer 5

1 in 10000 turned around so nucleus is 10 times smaller than the atom

diameter of atom is 10^-10m

diameter of nucleus therefore is 10^-14 m

Question 6

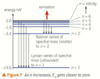
what happens to the deflection angle if the alpha particles are slowed done

how is scattering affected if the nuclei has less electric charge

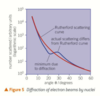
relationship between scatter angle and inverse square law

Answer 6

if alpha particles are slowed down more would be deflected at greater angles since the nucleus would be able to turn them back more easily

nuclei of smaller electric charge scatter alpha particles less strongly

the pattern of number of alpha particles scattered at different angles fits the pattern expected from the inverse square law for electric repulsion

Question 7

Answer 7

alpha particles are highly ionising and so will lose their energy over a short distance ionising air particles

by evacuating the apparatus (removing air particles) you cen minimise collisions and therefore get an accurate measure of the deflection angles

Question 8

kinetic energy of alpha particle at its closest approach

Answer 8

0 kinetic energy

Question 9

what is electrical potential energy equal to at a large distance from the nucleus

Answer 9

at a large distance from the nucleus, alpha particle electrical potential energy is equal to its initial kinetic energy

Question 10

equation for initial kinetic energy

charge on alpha particle

charge on gold particle

Answer 10

initial kinetic energy = electrical potential energy = kQq / r

alpha: 2e = 2 *(1.6*10^-19)
gold: 79e = 79 * (1.6*10^-19)

Question 11

force that a particle experiences near a nucleus

Answer 11

F = KQq / r²

Question 12

What did Rutherford discover about charge at the centre of the atom?

Answer 12

Some of the alpha particles were deflected through large angles, so the centre of the atom must have a large positive charge to repel them.

Question 13

What value do you need when you are estimating the distance of closest approach of an alpha particle that has been fired at a gold nucleus?

Answer 13

The alpha particles initial kinetic energy

Question 14

Answer 14

Question 15

What value do you need to find the charge of the nucleus?

Answer 15

The atom‘s proton number, Z

Question 16

how are electrons similar to alpha particles

Answer 16

electrons are scattered by the nucleus in the same way alpha particles are, but the force is attractive this time.

Question 17

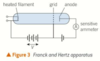
how to produce high energy electrons

Answer 17

using particle accelerators

Question 18

one application of particle accelerators

Answer 18

dental x-ray tubes are particle accelerators

electrons boiled off heated wire and accelerated towards positive target

Question 19

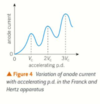
describe the change in energy for electrons in dental x-ray tubes

rearrange to give velocity

Answer 19

electrons lose electrical potential energy (qV) and gain kinetic energy (1/2mv²)

qV = 1/2mv²

can rearrange for v (velocity)

V = accel voltage

q = charge

m = mass of electron

Question 20

limitations of momentum equation

Answer 20

accurate at low speeds but not at high speeds

when v << c

Question 21

einstein momentum equation

Answer 21

momentum = relativistic factor * mass * velocity

Question 22

total energy of free particle

Answer 22

kinetic energy + rest energy

= relativistic factor * m * c²

Question 23

equation for energy when particle at rest

Answer 23

relativistic factor is 1 at rest so

Erest = mc²

Question 24

what is rest energy equivalent to

Answer 24

mass

Erest = m

Question 25

equation to calc relativistic factor using energy

Answer 25

rel factor = Etotal / Erest ymc² / mc²

Question 26

what is a linear accelerator and how does it work

Answer 26

a long straight tube containing electrodes which change charge signs electrons are acclerated between a pair of electrodes which have an alternating current applied to them its timed so that the electron is always attracted to the next electrode and repelled from the previous one length of electrodes increases because electrons are getting faster so they must stay in the tube for the same amount of time so that electrodes pd doesn't change too early the max speed of the electrons is only limited by the length of the accelerator, so they can approach the speed of light

Question 27

momentum approximation equation wavelength equation using this

Answer 27

when v is similar to c we can say momentum = y \* m \* v goes to momentum = y \* m \* c Etotal = y \* m \* c² so p = Etotal / c λ = h / p λ = h \* c / Etotal

Question 28

sin theta equation involving nuclear diameter

Answer 28

sin theta = 1.22(wavelength) / nuclear diameter can get wavelength from hc / E

Question 29

what are quarks

Answer 29

quarks are the building blocks for hadrons (protons and neutrons)

Question 30

how are quarks used to make protons and neutrons

Answer 30

to make the nucleons you need the 2 types of quark, the up quark (u) and the down quark (d) the up quark has charge 2/3 the down quark has charge -1/3 so proton = up(2/3) + up (2/3) + down (-1/3) = +1e neutron = ddu = -1/3 - 1/3 + 2/3

Question 31

how do you use quarks for antiprotons and antineutrons

Answer 31

an antiproton is a p with a line above it antineutron is a n with a line above it to make these you need antiquarks, quarks with the opposite charge these are the anti-up (-2/3) and anti-down (1/3) pic shows how to make them

Question 32

what holds quarks together inside a particle and how does it work

Answer 32

gluons are particles that are very strong and hold quarks together quarks attract one another by exchanging gluons gluons hold protons and neutrons in one piece keeping the nucleus together this interaction is known as the strong interaction

Question 33

antiparticle of electron how do antimatter differ from matter

Answer 33

the antiparticle equivalent of electron is the positron all antiparticles have the same mass as particles just the opposite charge

Question 34

2 ways to represent an alpha particle

Answer 34

⁴₂α ⁴₂He

Question 35

what are leptons what do they do example

Answer 35

leptons are fundamental particles that interact through a nuclear force called the weak interaction this weak interaction is reponsible for the beta decay electrons and neutrinos are leptons

Question 36

what are hadrons what do they do examples

Answer 36

hadrons are composite particles made up of quarks they interact through the strong interaction protons and neutrons are hadrons

Question 37

what are neutrinos

Answer 37

neutrinos are particles that you can assume to have 0 charge and 0 mass

Question 38

how are positrons emitted from a nucleus what happens after its been emitted what happens to the energy

Answer 38

in a process called beta decay (B+) a positron cannot exist in the world, almost instantly it encounters the outer electron of another particle and the 2 particles annihilate each other matter is destroyed, but energy can't be so all the mass of the particles gets converted to energy and is carried away by gamma rays travelling in opposite directions

Question 39

what is conserved during an annihilation event

Answer 39

electric charge linear and angular momentum energy lepton number

Question 40

lepton number for electron and positron

Answer 40

lepton number for electron: 1 lepton number for positron: -1

Question 41

what is pair creation what happens in it requirements

Answer 41

the opposite of annihilation creation of equal amounts of positron and electron by gamma ray photon of sufficient energy near a massive nucleus gamma ray photon must have energy equal or more to 2mc² (total rest energy of electron and positron) which is 1.022MeV

Question 42

why do you need a nucleus near a gamma photon to create an electron positron pair

Answer 42

a 1.022MeV gamma photon has enough energy to create an electron-positron pair but it can't create this in free space this is because the photon has momentum p = E / c and momentum must be conserved pair creation can occur near a nucleus which then carries away some momentum so that both energy and momentum is conserved lepton number and electric charge are conserved because the remain at 0

Question 43

how to find max lambda of gamma ray photon after electron and positron made from single gamma ray photon

Answer 43

E = 2mc² then E = hc / lambda rearrange and then calc for lambda

Question 44

what does a nucleus do when it has too many neutrons what is this process called

Answer 44

the nucleus has too many neutrons so it can decay by emitting an electron neutrins are unstable and decay into a proton this is beta minus decay (B-) n -\> p + e + antineutrino

Question 45

what is an issue with beta minus decay and what did it lead to the discovery of use the decay of strontium 90 to ytrrium 90 equation

Answer 45

⁹⁰₃₈Sr -\> ⁹⁰₃₉Y + ⁰_-1e neutron turns into proton to keep charge conserved and all numbers conserved electron (lepton) on right but no lepton (electron) on left difference in rest energy between Sr and Y but every beta particle doesn't have same energy as the difference so it was suggested that theres another particle emitted carrying the extra energy, no charge, small mass and weak interactions this is the neutrino (⁰₀v) so when the Sr decays to Y a beta particle is emitted along with an antineutrino (same as neutrino with a line above v) equation: ⁹⁰₃₈Sr -\> ⁹⁰₃₉Y + ⁰_-1e + (⁰₀v)line above v

Question 46

why is beta- decay not due to the strong interaction

Answer 46

n -\> p + e- + antineutrino electrons and v are leptons leptons are not affected by strong interaction, the decay can't be due to the strong interaction

Question 47

how are neon light signs evidence that electrons in atoms have discrete energy levels

Answer 47

their light comes in sharp discrete spectral lines

Question 48

how to find energy of photons given energy of 2 discrete energy levels

Answer 48

the energies of the photons correspond to the difference in energy levels in the atom

Question 49

describe the franck and hertz experiment

Answer 49

F and H experiment gives evidence for discrete energy levels tube filled with gas atoms that collide with electrons as they travel along the tube filament on left of tube is heated so electrons 'boiled off' and accelerated towards the wire grid at a certain positive potential. the anode will be at a slightly lower potential than the grid the difference in potential (e.g. 0.2V) is the minimum kinetic energy in electronvolts that electrons need to reach the anode (0.2eV) the current registered on the sensitive ammeter is a measure of the number of electrons passing through it each second

Question 50

fh exp: describe and explain the graph and what it gives evidence for

Answer 50

describe: increasing accelerating pd increases current but at Vc,2Vc and 3Vc current falls then rises exp: at low accelerating pds the electrons from the filament make elastic collisions with gas atoms bouncing off without loss of energy increasing pd increases the current registered on sensitive anode but at Vc, accel electrons have enough energy to knock an electron in the gas atom to a higher energy level, so some of the accel electron energy is given to the gas atom in an inelastic collision. this means some electrons don't have enough energy to reach the anode so current falls at 2 and 3Vc accel electrons can give energy to 2 or 3 atoms drops in current show inelastic collisions can only happen at specific electron energies. this shows that there are specific energy levels in the atom which the electrons are fixed to

Question 51

are electrons only allowed to have cerain energies

Answer 51

not really, because electrons have de broglie wavelengths associated with them atoms can be thought of having a potential energy well in which electrons are bound

Question 52

explain the standing wave for electrons with equation for energy of electrons

Answer 52

as electrons are trapped in the potential energy well of the positive nucleus standing waves for electrons can form de broglie wavelengths are limited by the size of the box we know p = h / lambda energy of electron is small so use non relativistic expression Ek = 1/2mv² = p² / 2m Ek = h² / 2mλ²

Question 53

how does the size of the box trapping the electron affect wavelength and energy and momentum how does it affect the fixed energy values

Answer 53

the smaller the box trapping the electron, the smaller the wavelength and so the greater the momentum and kinetic energy the size of the box determines the wavelength and so the allowed energy values

Question 54

hydrogen atom model for standing waves

Answer 54

applying model to hydrogen with a single electron with no potential wells but instead hard walls a fixed distance apart

Question 55

what does energy of electrons depend on in the hydrogen atom standing wave model what does this produce

Answer 55

the width of the box and the number n of half-wave loops in the standing waves produces a number of alowed energy levels labelled by a quantum number n at the ground state

Question 56

charge, and lepton number of proton, antiproton neutron, antineutron electron, positron neutrino, antineutrino

Answer 56

Question 57

how much energy do electrons need to escape the potential well in the wave model of the atom

Answer 57

has to have a total energy (Ek + Ep) of greater than 0

Question 58

using the de broglie wavelength equation how many wavelengths are there in n = 1 and 2 of the electron standing wave model

Answer 58

lambda = h / p = h / mv n = 1, half a wavelength between walls. lambda = 2d n = 2, one complete wavelength between walls, lambda = d n = 3, 2/3d

Question 59

Answer 59

force at right angles to direction of motion

Question 60

describe the process for annihilation in Positron Emission Tomography and then for brain tumour detecting

Answer 60

isotope of O2 gives off positron which interacts with outer electron of another atom, both destroyed in annihilation event, energy taken by gamma ray photons in brain tumours isotope of O2 injected into blood that gives out positrons while travelling throughout the body but a tumour will have a rich supply of blood so lots of decay there gives lots of gamma ray photons which leave head and are detected

Question 61

why does the graph look like this

Answer 61

electrons can show wave like properties the red line is if electrons act like the particles that they are the blue line is the actual scattering due to electron diffraction showing the 'kinks' in the curve electrons follow rutherford's scattering but the curve superimposed on it is the diffraction pattern because electrons act in a wave like manner

Question 62

if given graph similar to this how do I work out nuclear diameter of particles

Answer 62

look for lowest kink on diagram and read at what angle that is on the graph nuclear diameter = 1.22lambda / sin theta lambda = hc / E

Question 63

describe bubble chambers and what they do

Answer 63

in bubble chambers fast particles ionise water vapour creating a trail there are 2 trails due to the charge on the particle one due to +ve charge and the other -ve charge inwards spiralling because they're losing energy

Question 64

kinetic energy for electron using de broglie wavelength

Answer 64

Question 65

as only certain wavelengths can fit in an electron how is ke affected

Answer 65

only certain wavelengths of electrons can fit inside atoms at a certain distance from nucleus ke is also limited to certain energies

Question 66

what does En = -13.6eV / n show find out En when n = 1 and 2

Answer 66

this shows the energy required for energy levels for hydrogen where n is the energy level so n = 1 at ground state when n = 1, En = -13.6eV / 1² = -13.6eV when n = 2, En = -13.6eV / 2² = -3.4eV

Question 67

what happens when an electron goes from a higher energy orbit to a lower energy orbit

Answer 67

electric potential energy gets more negative the change in energy is the energy of the photon emitted

Question 68

find the wavelength of the photon emitted when an electron falls from n = 3 to 1

Answer 68

n = 3 = -1.5eV n = 1 = -13.6eV change in energy = 12.5eV \* 1.6 \* 10^-19 = 1.936 \* 10^-18J photon energy E E = hc / lambda lambda = hc / E = 1 \* 10-7m visible light = 400Nm to 700Nm this is below it so its in the UV range this is correct as drop from n = 3 to n = 1 is in the lyman series

Question 69

why is an electron better for diffraction compared to alpha particles

Answer 69

electrons aren't affected by strong nuclear force so they can touch the nucleus and turn around whereas alpha particles would be captured by gluons and absorbed into the nucleus

Question 70

quick way to calculate velocity with a known value of relativistic factor

Answer 70

v / c = ROOT(1 - 1 / (rel factor)²)