Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

A1-Phys-23-1-D1 > ch11 > Flashcards

ch11 Flashcards

1
Q

conditions for simple harmonic motion

A

force is directly proportional to displacement, and the acceleration (force) acts in the opposite direction to the displacement this tells us force is always directed to the position of equilibrium

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

examples of simple harmonic oscillators

A

springs and pendulums

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

what is the time for one complete swing of an oscillator

A

time period

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

what is the amplitude of an oscillation

A

greatest displacement from the equilibrium position

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

what is simple harmonic motion

A

an oscillation in which the restoring force on an object (acceleration of the object) is directly proportional to it’s displacement from the centre, and is directed towards the centre

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

equation for angular frequency, w, rate of rotation

A

w = 2πf rad s^-1

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

versions of equation for displacement applying angular velocity disp = max at t = 0 disp = 0 at t = 0

A

if displacement is at max when t = 0 use the equation x = Acos(2πft) -> x = Acos(wt) if displacement is 0 when t = 0 x = Asin(2πft) -> x = Asin(wt) x = displacement in metres A = amplitude t = time in seconds

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

how to calculate acceleration using angular velocity and the differentiation model for disp to accel

A

a = -w²x = -4π²f²x = d²x / dt²

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

what does a negative value mean when you calculate displacement of an object using the displacement equation x = Acos(2πft)

A

the mass is below the equilibrium at that point in instant

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

what is the acceleration at the point in equilibrium and why is this

A

acceleration at the point of equilibrium is 0, as x = 0 and a ∝ -x

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

a simple harmonic oscillator has an amplitude of 0.02m, the frequency of the oscillation is 1.5Hz calculate the maximum acceleration

A

maximum acceleration is at max displacement as a ∝ -x so x is 0.02 a = -4 * π² * f² * 0.02 = -1.8 ms^-2

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

displacement, x, against time graph for SH oscillator max disp at t = 0 T = 2π what type of graph is it

A

when amplitude A is max (max displacement) at t = 0, it’s a cosine graph

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

velocity, v, against time graph for SH oscillator max disp at t = 0 T = 2π what type of graph is it

A

the graph of velocity is the gradient of the displacement graph at t = 0, disp graph has max displacement so velocity starts at 0 the graph of velocity is a reflection of sin x in the x-axis (-sinx)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

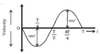
acceleration, a, against time graph for Sh oscillator max disp at t = 0 T = 2π what type of graph is it

A

the graph of acceleration is the gradient of the velocity graph at t = 0, displacement graph has max displacement so velocity is 0 and as velocity is 0, acceleration starts at minimum value the graph of acceleration is a reflection of cos x in the x-axis (-cosx) the graph of acceleration is also the opposite of the displacement graph

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

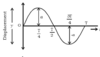
displacement, x, against time graph for SH oscillator min displacement at t = 0 T = 2π what type of graph is it

A

at t = 0, displacement is 0 (0 amplitude A) it’s a normal sin x graph

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

velocity, v, against time graph for SH oscillator min displacement at t = 0 T = 2π what type of graph is it

A

the graph of velocity is the gradient of the displacement graph at t = 0, disp graph has 0 displacement so velocity starts at max value it’s a cosine graph

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

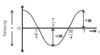
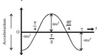
acceleration, a, against time graph for SH oscillator min displacement at t = 0 T = 2π what type of graph is it

A

the graph of acceleration is the gradient of the velocity graph at t = 0, displacement graph has 0 displacement so velocity is at max acceleration graph is the opposite of the displacement graph, but as displacement is 0, acceleration starts at 0 a = -x acceleration is a reflection of the displacement graph

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

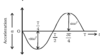
value of velocity when displacement is maximum

A

0

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

value of velocity when displacement is 0

A

maximum

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

value of displacement when velocity is 0

A

maximum

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

value of displacement when velocity is maximum

A

0

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

what equation can be used to calculate acceleration, and thus velocity and displacement, from iterative models and calculations

A

F = ma

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q

maximum value of acceleration graph

A

w²A

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
Q

maximum value of velocity graph

A

wA

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
25
Q

maximum value of displacement graph

A

A

26
Q

equation for oscillation of a mass on a spring with a restoring force (acceleration to the equilibrium) proportional to displacement

A

a = -kx / m = Δ²x / Δt²

27
Q

equation for force exerted when a mass is pushed between springs

A

F = kx

F = force in netwons

k = spring constant

x = displacement in metres

28
Q

equation for time period of a mass oscillating on a spring

A

T = 2π (√m / k)

T = period of oscillation in seconds

m = mass in kg

k = spring constant

29
Q

link between time period of the oscillation and the mass of spring

A

t² ∝ m

30
Q

link between time period of oscillation of spring and the spring constant

A

T² ∝ 1 / k

31
Q

link between time period of oscillation of mass on a spring and amplitude

A

Time doesn’t depend on amplitude A

32
Q

equation for elastic strain energy a spring gains from compressing or stretching

A

E = 1/2 * k * x²

E = elastic energy in joules

k = spring constant

x = displacement in metres

33
Q

what type of energy do you need to take into account when calculating elastic energy gained for a spring that’s oscillating vertically

A

graviational potential energy must be taken into account for a spring oscillating vertically

34
Q

equation for time period of a pendulum

up to what angles of oscillation does this equation apply

A

T = 2π (√L / g)

T = time period in seconds

L = length of pendulum in metres

g = gravitational field strength Nkg^-1

35
Q

why will a pendulum clock keep ticking in regular time intervals even if its swing becomes very small

A

in SHM, the frequency and period are independent of the amplitude

(constant for a given oscillation)

36
Q

modelling equation for SHM: force (acceleration) and displacement link

A

since F = ma = m(d²x / dt²)

F = -kx

so:

(d²x / dt²) = -k/m x

37
Q

equation to work out change in velocity in a fixed time interval

A

Δv = -(k/m)x Δt

38
Q

equation for change in displacement compared to v over a fixed time interval

A

v = Δx / Δt

Δx = vΔt

39
Q

limitation of simple mathematical model

A

when run for a long time, it produces an ever increasing amplitude which is not what happens in simple harmonic oscillation, so it’s a limitation of the simple model

40
Q

equation for velocity (speed) and max velocity

A

V = +- 2πf (√A² - x²)

Vmax = +- 2πfA

41
Q

how to work out amplitude of a pendulum from equilibrium if you’re given height diffrerence

A

you have to get it through energy. at that heigh difference it has no kinetic energy, but it has gravitational potential energy, mgh

when it goes back to equilibrium it has kinetic energy

mgh = 1/2m (Vmax)²

gh = 1/2 (Vmax)²

42
Q

equation for tension in pendulum’s string

A

Tension = mg to hold pendulum in place

there’s also circular motion

T = mg + mv² / r

43
Q

velocity and acceleration of oscillators at any given time with sin and cos

A

v = sin 2πft

a = cos2πft

44
Q

features of free oscillations

A

constant amplitude

no resultant driving force

vibrates at it’s natural frequency

45
Q

features of forced oscillations

A

have a driving force, without the driving force the oscillations would slow to a stop

46
Q

what is resonance

A

if the driving frequency (frequency of the driving force, an external force) matches the natural frequency of the object / system, resonance occurs.

this causes amplitude of oscillations to rapidly increase

the amplitudes will rise until the energy losses

47
Q

what happens if a system is only lightly damped and it starts resonating

A

the increase in aplitude due to resonating will still be dramatic

48
Q

what is damping

A

the reverse of resonance.

occurs when energy is lost from an oscillating system, causing amplitude to decrease to 0

usually due to frictional forces like air resistance

49
Q

levels of dampening for oscillation along with descriptions

A

lightly damped -

decrease to 0 is gradual, max displacement reduces every oscillation, but the time period is near constant

critically damped -

zero amplitude is reached in the shortest time, oscillator stops at equilibrium without even finishing a cycle

heavily damped (overdamped) -

decrease of displacement is slow and return to equilibrium takes a lot longer

50
Q

why are systems damped?

A

to stop them oscillating or to minimise resonance effects

51
Q

what happens when the driving frequency exceeds the natural frequency

and how does more damping help

A

the amplitude of the oscillation is even lower than without a driving force

more damping decreases the maximum resonance and there’s a broader maximum peak

52
Q

equation for energy stored by a SHO

A

E = 1/2 K A²

53
Q

equation for max acceleration

A

at a(max) acceleration is mas as displacement is max so accel = A

a(max) = -4π²f²A

54
Q

kinetic energy when the osciallator passes through the equilibrium position

A

at x = 0

all the energy is kinetic energy , Ek

55
Q

total energy of an oscillator any point

A

Etotal = 1/2 K A² = 1/2Ek + 1/2Ep

Etotal = 1/2mv² + 1/2kx²

56
Q

how to find max kinetic energy (total energy) at equilibrium for a swinging pendulum

A

Kemax = 1/2mvmax²

vmax = 2πfA

so:

Kemax = mπfA

57
Q

why lines of displacement in an oscillator are curves

A

kinetic energy is proportional to velocity² (1/2mv²)

and velocity depends on displacement

so kinetic energy is proportional to displacement²

58
Q

how do you work out total energy of the system

A

try find out what Vmax is (2πfA)

and then you can plug it into Kemax = 1/2mvmax²

59
Q

for this simple pendulum the maximum height h above the equilibrium position where the 2 orange balls are is 0.02m

the mass of the pendulum bob is 0.05kg

on the far left is A, on the far right is C, and in the middle is B

describe the changes between GPE and KE as the pendulum bob moves between point A and B

A

At point A the bob is instantaneously stationary at its maximum height h, so it has 0 kinetic energy and maximum gravitational potential energy

as it goes back towards the position of equilibrium, it is accelerating and so gaining kinetic energy while losing GPE

once it has reached it, kinetic energy is at maximum, while h is 0 so GPE is 0 relative to the point of equilibrium

60
Q

for a simple pendulum the max height h above equilibrium is 0.02m and the mass of the bob is 0.05kg

calculate the total energy of the system

A

total energy of the system = maximum potential energy

Etotal = 0.05kg * 9.8N kg^-1 * 0.02m = 9.8 * 10^-3 J

61
Q

pendulum has heigh h above equilibrium of 0.02m, mass of pendulum bob is 0.05kg

calculate velocity of bob as it passes through equilibrium

A

at equilibrium, kinetic energy = max and GPE = 0,

so kinetic energy is the total energy, 9.8 * 10^-3 J

1/2mv² = 9.8 * 10^-3 J

v = (√(2 * 9.8 *10^-3) / 0.05kg) = 0.63ms^-1

A1-Phys-23-1-D1 (61 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions