Ch. 7 - Functions Flashcards
(15 cards)
Even Function
A function of which ƒ(x) = ƒ(-x).
Even functions are symetrical across the y-axis.
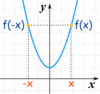
Odd Function
A function for which -ƒ(x) = ƒ(-x)
Odd functions have origin symmetry, which means that they are the same when reflected across the origin.

Root
Values in a function’s domain at which the function eqauls zero.
A root is also called a zero, solution, or x-intercept of a function.
Frequency
The number of times a graph repeats itself in a given distance;
the reciprical of the function’s period
Inverse Functions
An inverse function always deso the opposite of each opperation in the original function, in reverse order.
Inverse Compound Functions
If ƒ(g(x)) = x,
then g(x) = ƒ-1(x).
Mathematical Impossibilites for Domain
- A fraction havinga denominator of zero.
- Any even-numbered root of a negative number.
Rules that limit a function’s range
- An even exponent produces only nonnegative numbers.
- The even-numbered root of a quanitity represents only the positive root.
- Absolute values produce only nonnegative values.
A nonnegative operation has a range of {ƒ(x) ≥ 0}. When an opperation is applied to the function (i.e. * -1, + c, * a), the range is also effected in the same way.
To estimate range and domain based on a function’s graph, use these rules…

Periodic Function
A function that repeats a pettern of range values forever.

Movement of a function

Algebraic meaning of the degree of a function
It equals the maximum munber of roots that a function has.
What is the degree of the term:
3xy2
The degree of that term is 3
The degree of a term in a polynomial is the sum of the exponents of the variables in that term.
How distinct roots does the following have?
ƒ(x) = x6
g(x) = (x–1)(x–2)(x–3)(x–4)(x–5)(x–6)
ƒ(x) has one distinct root.
g(x) has six distinct roots.
An nth-degree function has a maximum of n distinct roots and a maximum of (n – 1) local extreme values.



