Ch. 4 - Solid Geometry Flashcards
(21 cards)
Volume of a prism
Prisms are three-dimentional figures that have two parallel, identical bases that are polygons.
V = Bh
B represents the area of the base of the prism, and h represents the height of the prism.
Volume of a rectangular solid
V = lwh
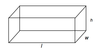
Surface area of a Rectangular Solid
SA = 2lw + 2wh + 2lh
Long Diagonal of a Rectangular Solid
(Super Pythagorean Theorem)
l2 + w2 + h2 = d2

Volume of a Cube
V = s3
Surface Area of a Cube
SA = 6s2
Face Diagonal of a Cube
ƒ = s√2
Long Diagonal of a Cube
d = s√3
Volume of a Cylinder
V = πr2h
Surface Area of a Cylinder
SA = 2πr2 + 2πrh
Longest line that can be drawn inside a cylinder
d2 = (2r)2 + h

Voume of a Cone
V = 1/3 πr2h
(just one-third the volume of a circular cylinder)
Surface Area of a Cone
SA = πrl + πr2

Volume of a Sphere
V = 4/3 πr3
Surface Area of a Sphere
SA = 4πr2
Volume of a Pyramid
V = 1/3 Bh
(B = area of base)
(Just one-third of the volume of a prism)
When a cube or rectangle solid is inscribed in a sphere, the long diagonal of the solid is equal to the diameter of the sphere.
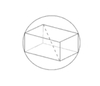
When a cylinder is inscribed in a sphere, the sphere’s diameter is equal to the diagonal of the rectangle formed by the cylinder’s heights and diameter.
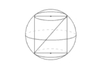
When a sphere is inscribed in a cube, the diameter of the sphere is equal to the length of the cubes edge.

If a sphere is inscribed in a cylinder, both solids have the same diameter.

When the lengths of a solid are increased by a certain factor, the surface area of the solid increases by the square of that factor, and the volume increases by the cube of that factor. This rule is true only when the solid’s shape doesn’t change—its length must increase in every direction, not just one.