Booklet 3 - Electricity (Worked Examples)

Question 1

Use the oscilloscope trace to calculate

(a) the frequency
(b) the peak voltage

Answer 1

(a) The distance between crests is 4 cm.
The time base is set at 5 ms cm^–1
The period of the wave is
T = 4 x 5ms = 4 0.005s = 0.02 s
f = 1/T
f = 1/0.02
f = 50 Hz

(b) The height from bottom to top is 8 cm.
The height from middle to top is ½ × 8 = 4 cm
The volts/div was set at 2 V cm^–1,
The peak voltage is:
V_peak = 4 × 2
V_peak = 8 V

Question 2

A power pack is labelled with a voltage of 12 V r.m.s.
Calculate the peak voltage.

Answer 2

V_peak = √2 x V_rms
V_peak = 1.41 x 12
= 17.0 V

Question 3

Example

Calculate the current flowing during a bolt of lightning which lasts for 10 ms and transfers 50 C of charge.

Answer 3

Q = 50 C

I = ?

t = 10 ms = 10 x 10^-3 s

Q = It

50 = I x 10 x 10^-3

I x 10 x 10^-3 = 50

I = 50/10 x 10^-3

I = 5000 A

Question 4

Example

Calculate the current flowing when a 2 kΩ resistor is connected to a 6V battery.

Answer 4

V = 6 V

I = ?

R = 2 kΩ = 2 x 10³ Ω

V = IR

6 = I x 2 x 10³

I x 2 x 10³ = 6

I = 6/2 x 10³

I = 3 x 10^-3 A

Question 5

Example

Calculate the current drawn when a 2 kW kettle is plugged into the mains.

Answer 5

P = 2 kW = 2000 W
I = ?
V = 230 V (UK Mains Voltage - see previous LO)

P = IV
2000 = I x 230
I x 230 = 2000
I = 2000/230
I = 8.70 A (to 3 sig fig)

Question 6

Example

Calculate the current flowing when 3500 W of power are supplied to a 100 Ω resistor.

Answer 6

P = 3500 W
I = ?
R = 100 Ω

P = I²R
3500 = I² x 100
I² x 100 = 3500
I² = 3500/100
I² = 35
I = √35
I = 5.92 A (to 3 sig fig)

Question 7

Example

A 100 Ω resistor is attached to a 9 V battery. Calculate the power supplied.

Answer 7

P = ?
V = 9 V
R = 100 Ω

P = V<sup>2</sup>/R
P = 9<sup>2</sup>/100
P = 81/100
P = 0·81 W

Question 8

Example

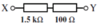
Calculate the total resistance of the circuit shown.

Answer 8

R<sub>T</sub> = ?
R<sub>1</sub> = 1·5 kΩ = 1500 Ω
R<sub>2</sub> = 100 Ω

R<sub>T</sub> = R<sub>1 </sub>+ R<sub>2 </sub>+ ....
R<sub>T</sub> = 1500 + 100
R<sub>T</sub> = 1600 Ω

Question 9

Example

Calculate the total resistance of the circuit shown.

Answer 9

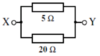
RT = ?
R1 = 5 Ω
R2 = 20 Ω

1/R<sub>T</sub> = 1/R<sub>1 </sub>+ 1/R<sub>2 </sub>+ ....
1/R<sub>T</sub> = 1/5 + 1/20
1/R<sub>T</sub> = 1/4
R<sub>T</sub> = 4/1 = 4 Ω

Question 10

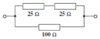
Example

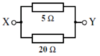
Calculate the total resistance of the circuit shown.

Answer 10

25 & 25 in series

RT = ?
R1 = 25 Ω
R2 = 25 Ω

R<sub>T</sub> = R<sub>1 </sub>+ R<sub>2 </sub>+ ....
R<sub>T</sub> = 25 + 25
R<sub>T</sub> = 50 Ω

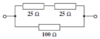
50 (above) in parallel with 100

RT = ?
R1 = 50 Ω
R2 = 100 Ω

1/R<sub>T</sub> = 1/R<sub>1 </sub>+ 1/R<sub>2 </sub>+ ....
1/R<sub>T</sub> = 1/50 + 1/100
1/R<sub>T</sub> = 3/100
R<sub>T</sub> = 100/3 = 33.3 Ω (to 3 sig fig)

Question 11

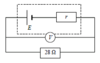
A cell of emf 1.5 V is connected in series with a 28 Ω resistor. A voltmeter measures the
voltage across the cell as 1.4 V.
Calculate:
(a) the internal resistance of the cell
(b) the current if the cell terminals are short circuited
(c) the lost volts if the external resistance R is increased to 58 Ω.

Answer 11

(a) E = 1.5 V
R = 28 Ω
V = 1.4 V

In this case we do not know the current, I, but we can work it out:
V = IR
1.4 = I x 28
I = 0.05 A

E = V + Ir
1.5 = 1.4 + 0.05 x r
r = 2 Ω

(b) Short circuit: R = 0, V = 0; Assume E (1.5 V) and r (2 Ω) constant
E = V + Ir
1.5 = 0 + I x 2
I = 0.75 A

(c) Assume E (1.5 V) and r (2 Ω) constant
Combine E = V + Ir and V = IR to get E = I(R + r)
1.5 = I x (58 + 2)
I = 1.5/60 = 0.025 A
lost volts = Ir
= 0.025 × 2
= 0.05 V

Question 12

Example

Calculate V₁ in this circuit.

Answer 12

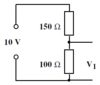
V<sub>1</sub> = ?
R<sub>1</sub> = 100 Ω (This is R<sub>1</sub> because it has been marked as V<sub>1</sub> in the question)
R<sub>2</sub> = 150 Ω
V<sub>s</sub> = 10 V

V<sub>1</sub> = R<sub>1</sub>/(R<sub>1</sub>+R<sub>2</sub>) x V<sub>s</sub>
V<sub>1</sub> = 100/(100+150) x 10
V<sub>1</sub> = 4 V

(NB The formula sheet uses V₂ = R₂/(R₁+R₂) x V_s but this can be adapted as above as long as the voltage and resistor in bold agree with each other i.e.
V₁ = R₁/(R₁+R₂) x V_s
or
V₂ = R₂/(R₁+R₂) x V_s

The choice of which resistor is labelled 1 or 2 doesn’t matter unless it has already been marked in the Q)

Question 13

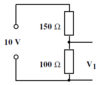
Example

Calculate V₁ in this circuit.

Answer 13

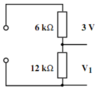
V₁ = ?
V₂ = 3 V
R₁ = 12 kΩ
R₂ = 6 kΩ
​(Can leave R₁ and R₂ in kΩ since the formula is a ratio.)

V<sub>1</sub>/V<sub>2</sub> = R<sub>1</sub>/R<sub>2</sub>
V<sub>1</sub>/3 = 12/6
V<sub>1</sub> = 3x12/6
V<sub>1</sub> = 6 V

Question 14

A circuit is attached to XY which has a resistance of 10 kΩ. Calculate the effective
resistance between XY and thus the voltage across XY.

Answer 14

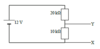
The resistance between XY comes from the two identical 10 kΩ resistors in parallel.
The combined resistance is therefore 5 kΩ (You can check this using 1/R_T = 1/R₁ + 1/R₂).
Use this resistance as R₁ in the potential divider formula.
R₁ = 5 kΩ
R₂ = 20 kΩ
V_S = 12 V
V₁ = ?

V<sub>1</sub> = R<sub>1</sub>/(R<sub>1</sub> + R<sub>2</sub>) x V<sub>s</sub>
V<sub>1</sub> = 5/(5 + 20) x 12
V<sub>1</sub> = 2.4 V

Question 15

A capacitor stores 4 x 10^-4 C of charge when the potential difference across it is 100 V.

(a) Calculate the capacitance.
(b) Calculate the energy stored in the capacitor.

Answer 15

C = ?
Q = 4 x 10<sup>-4</sup> C
V = 100 V

(a) C = Q/V
= 4 x 10^-4/100
= 4 x 10^-6 F

(b) E = ½QV
E = ½ x 4 x 10^-4 x 100
E = 0.02 J

Question 16

A 40 µF capacitor is fully charged using a 50 V supply.

Calculate the energy stored in the capacitor.

Answer 16

E = ?
C = 40 µF = 40 x 10<sup>-6</sup> F
V = 50 V

E = ½ CV<sup>2</sup>
E = ½ x 40 x 10<sup>-6</sup> x 50<sup>2</sup>
E = 0.05 J

Question 17

A 50 µF capacitor stores 2 mC of charge when fully charged.

Calculate the energy stored in the capacitor.

Answer 17

E = ?
Q = 2 mC = 2 x 10<sup>-3</sup> C
C = 50 µF = 50 x 10<sup>-6</sup> F

E = ½ Q<sup>2</sup>/C
E = ½ x (2 x 10<sup>-3</sup>)<sup>2</sup> / 50 x 10<sup>-6</sup>
E = 0.04 J