Booklet 2B - Waves (Worked Examples) Flashcards
(7 cards)

A diffraction grating with 300 lines per mm is used to produce an interference pattern. The
second order maximum is obtained at a diffracted angle of 19°.
Calculate the wavelength of the light.
m = 2 θ = 19°
Find the refractive index of the clear plastic using the information given in the
diagram:

Angles need to be measured relative to the normal:
θ1 = 90 - 30 = 60°
θ2 = 90 - 54 = 36°
n = sinθ1/sinθ2
n = sin60/sin36
n = 1.47
Monochromatic blue light of wavelength 500 nm in air is incident on glass. The refractive index of blue light for this glass is 1.53. Find
(a) the frequency of blue light in air and in glass
(b) the speed of the light in glass
(c) the wavelength of the light in
the glass.
λ<sub>1</sub> = 500 nm = 500 x 10<sup>-9</sup> m n = 1.53 v<sub>1</sub> = 3.00 x 10<sup>8</sup> ms<sup>-1</sup> (speed of light in air)
(a) In air
v1 = fλ1
3.00 x 108 = f x 500 x 10-9
f = 6 x 1014 Hz
f in glass is the same i.e. 6 x 1014 Hz
(b) n = sinθ1/sinθ2 = v1/v2 = λ1/λ2
n = v1/v2
1.53 = 3.00 x 108/v2
v2 = 1.96 x 108 ms-1
(c) n = sinθ1/sinθ2 = v1/v2 = λ1/λ2
n = λ1/λ2
1.53 = 500 x 10-9/λ2
λ2 = 3.26 x 10-7 m
A ray of light is incident on the inside surface
of a glass block of refractive index 1.50. Is
the light refracted or totally internally reflected?
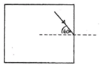
n = 1.5 θ<sub>c</sub> = ?
sin θc = 1/n
sin θc = 1/1.5
θc = 42°
The angle of incidence is 60°, which is greater than 42°,
so total internal reflection takes place in this case.
Alternatively, assume refraction takes place:
n = 1.5
n = sinθ1/sinθ2
1.5 = sinθ1/sin60
sinθ1 = 1.3
but this is impossible since sinθ1 cannot be greater than 1. This tells you that total
internal reflection occurs, and there is no refraction.
A bulb (generally assumed to be a point source from a reasonable distance away) shines onto
a screen of area 2.5 m2 which is 3 m away. The irradiance at the screen is 0.01 Wm-2.
(a) Calculate the power incident on the screen.
(b) If the screen was moved to 1.5 m from the bulb, what would be the new irradiance at the screen?
A = 2.5 m<sup>2</sup> d<sub>1</sub> = 3 m I = 0.01 Wm<sup>-2</sup>
(a) I = P/A
0.01 = P/2.5
P = 0.025 W
(b) From I = k/d2, Id2 = k so I1d12 = I2d22
0.01 x 32 = I2 x 1.52
I2 = 0.04 Wm-2
The diagram shows energy levels for the helium atom.
(a) Calculate the frequency of the emission transition shown.
(b) Calculate the frequency of the absorption transition shown.
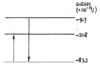
(a) The emission transition occurs when an electron loses energy i.e. the downwards arrow
E2 = -9.7 x 10-19 J
E1 = -87.2 x 10-19 J
h = 6.63 x 10-34 J s (from data sheet)
E2 - E1 = hf
-9.7 x 10-19 - (-87.2 x 10-19) = 6.63 x 10-34 x f
f = 1.17 x 1016 Hz
(b) The absorption transition occurs when an electron gains energy i.e. the upwards arrow
E2 = -21.8 x 10-19 J
E1 = -87.2 x 10-19 J
h = 6.63 x 10-34 J s (from data sheet)
E2 - E1 = hf
-21.8 x 10-19 - (-87.2 x 10-19) = 6.63 x 10-34 x f
f = 9.86 x 1015 Hz


