Basics Of Optimization

Question 1

Loss function (Objective function)

Answer 1

An optimization problem has an objective function that is defined in terms of a set of variables, referred to as optimization variables. The goal of the optimization problem is to compute the values of the variables at which the objective function is either maximized or minimized.

Question 2

Optimality Conditions in Unconstrained Optimization

Answer 2

A univariate function f(x) is a minimum value at x = x₀ with respect to its immediate locality if it
satisfies both f
(x₀)=0 and f(x₀) > 0.

Question 3

Taylor expansion for evaluating minima

Answer 3

Question 4

Jacobian

Answer 4

Question 5

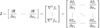
Hessian matrix

Answer 5

Question 6

Multivariate Taylor expansion for evaluating minima

Answer 6

Question 7

Second-order optimality conditions

Answer 7

Question 8

Convex set

Answer 8

A set S is convex, if for every pair of points w₁, w₂ ∈ S, the point λw₁ + [1 − λ]w₂ must also be in S for all λ ∈ (0, 1)

Question 9

Convex set - Visual representation

Answer 9

Question 10

Convex function

Answer 10

Question 11

Linear functions and convexity

Answer 11

A linear function of the vector w is always convex

Question 12

Second-Derivative Characterization of Convexity

Answer 12

The twice differentiable function F(w) is convex, if and only if it has a positive semidefinite Hessian at every value of the parameter w in the domain of F(·)

Question 13

The following convexity definitions are equivalent for twice differentiable functions defined over R^d

Answer 13

Question 14

The sum of a convex function and a strictly convex function

Answer 14

Is strictly convex

Question 15

Finite-difference approximation

Answer 15

Is used to verify that the gradient is calculated appropriately

Question 16

Decaying learning rate

Answer 16

Question 17

The gradient at the optimal point of a line search

Answer 17

Is always orthogonal to the current search direction

Question 18

Second-order multivariate Taylor expansion of J(w) in the immediate locality of w₀ along the direction v and small radius ε > 0

Answer 18

Question 19

Mini-batch stochastic gradient descent

Question 20

Min-max normalization

Answer 20

Min-max normalization is useful when the data needs to be scaled in the range (0, 1)

Question 21

Feature normalization

Answer 21

A common type of normalization is to divide each feature value by its standard deviation. When this type of feature scaling is combined with mean-centering, the data is said to have been standardized. The basic idea is that each feature is presumed to have been drawn from a standard normal distribution with zero mean and unit variance

Question 22

Mean-centering

Answer 22

In many models, it can be useful to mean-center the data in order to remove certain types of bias effects. Many algorithms in traditional machine learning (such as principal component analysis) also work with the assumption of mean-centered data. In such cases, a vector of column-wise means is subtracted from each data point

Question 23

Common quadratic loss function and its gradient

Answer 23

Question 24

Common linear loss function and its gradient

Answer 24

Question 25

Commonly used matrix calculus identities - numerator layout

Answer 25

Question 26

Commonly used matrix calculus identities - denominator layout

Answer 26

Question 27

Commonly used matrix calculus identities - denominator layout (objective functions and vector-to-vector)

Answer 27

Question 28

Unconstrained quadratic program

Answer 28

Question 29

Optimality condition and solution to the quadratic program

Answer 29

Question 30

1-dimensional and multidimensional quadratic functions minimum

Answer 30

An unconstrained quadratic program is a direct generalization of 1-dimensional quadratic functions like 1/2ax² + bx + c. Note that a minimum exists at x = −b/a for 1-dimensional quadratic functions when a \> 0, and a minimum exists for multidimensional quadratic functions when A is positive definite

Question 31

Squared norm objective function and gradient

Answer 31

Question 32

Univariate chain rule

Answer 32

Question 33

Chain rule where one of the functions is a vector-to-scalar function

Answer 33

Question 34

Least-square regression objective function

Answer 34

Question 35

Tikhonov Regularization

Answer 35

Question 36

Normal equation with Tikhonov regularization

Answer 36

Question 37

Jacobian, Gram matrix and Normal Equation relation

Answer 37

Question 38

Covariance Matrix of Mean-Centered Data

Answer 38

The unscaled version of the matrix, in which the factor of n is not used in the denominator, is referred to as the scatter matrix. In other words, the scatter matrix is simply D^TD. The scatter matrix is the Gram matrix of the column space of D, whereas the similarity matrix is the Gram matrix of the row space of D

Question 39

Regularized weight vector

Answer 39

Question 40

Stochastic and mini-batch gradient descent with regularization

Answer 40

Question 41

L₂-loss SVM

Answer 41

Question 42

Hinge-loss SVM (L₁-loss)

Answer 42

Question 43

Point-wise loss derivatives for the L1 (hinge) and L₂ loss

Question 44

Logistic regression loss

Answer 44

Question 45

Mini-batch stochastic gradient-descent for the logistic function

Answer 45

Question 46

Multi-class SVM loss function with regularization

Answer 46

Question 47

Loss function and stochastic gradient descent for the multi-class SVM

Answer 47