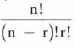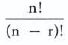(8) Probability Concepts Flashcards
LOS 9. a: Define a random variable, an outcome, an event, mutually exclusive events, and exhaustive events.
A random variable is an uncertain value determined by chance.
An outcome is the realization of a random variable.
An event is a set of one or more outcomes. Two events cannot both occur are termed “mutually exclusive” and a set of events that includes all possible outcomes is an “exhaustive” set of events.
LOS 9. b: State the two defining properties of probability and distinguish among empirical, subjective, and a priori probabilities.
The two properties of probability are:
- The sum of the probabilities of all possible mutually exclusive events is 1.
- The probability of any event cannot be greater than 1 or less than 0.
A priori probability measures predetermined probabilities based on well-defined inputs;
Empirical probability measures probability fo4m observations or experiments;
And subjective probability is an informed guess.
LOS 9. c: State the probability of an event in terms of odds for and against the event.
Probabilities can be stated as odds that an event will or will not occur. If the probability of an event is A out of B trails (A/B), the “odds for” are A to (B-A) and the “odds against” are (B-A) to A.
Example 1/6, odds for 1:7, odds against 7:1.
LOS 9. d: Distinguish between unconditional and conditional probabilities.
Unconditional probability (marginal probability) is the probability of an event occurring.
Conditional probability, P(A|B), is the probability of an event A occurring given that event B has occurred.
LOS 9. e: Explain the multiplication, addition, and total probability rules.
The multiplication rule of probability is used to determine the joint probability of two events:
P(AB) = P(A|B) x P(B)
LOS 9. e: Explain the multiplication, addition, and total probability rules.
The addition rule of probability is used to determine the probability that at least one of two events will occur:
P(A or B) = P(A) + P(B) – P(AB)
LOS 9. e: Explain the multiplication, addition, and total probability rules.
The total probability rule is used to determine the unconditional probability of an event, given conditional probabilities:
P(A) = P(A|B1) x P(B1) + P(A|B2) x P(B2) + … + P(A|BN) x P(BN)
Where B1, B2, …, BN is a mutually exclusive and exhaustive set of outcomes.
LOS 9. f: Calculate and interpret 1) the joint probability of two events, 2) the probability that at least one of two events will occur, given the probability of each and the joint probability of the two events, and 3) a joint probability of any number of independent events.
The joint probability of two events P(AB), is the probability that they will both occur. P(AB) = P(A|B) x P(B).
For independent events, P(A|B) = P(A), so that P(AB) = P(A) x P(B).
LOS 9. f: Calculate and interpret 1) the joint probability of two events, 2) the probability that at least one of two events will occur, given the probability of each and the joint probability of the two events, and 3) a joint probability of any number of independent events.
The probability that at least one of two events will occur is P(A or B) = P(A) + P(B) – P(AB). For mutually exclusive events, P(A or B) = P(A) + P(B), since P(AB) = 0.
LOS 9. f: Calculate and interpret 1) the joint probability of two events, 2) the probability that at least one of two events will occur, given the probability of each and the joint probability of the two events, and 3) a joint probability of any number of independent events.
The joint probability of any number of independent events is the product of their individual probabilities.
LOS 9. g: Distinguish between dependent and independent events.
The probability of an independent event is unaffected by the occurrence of other events, but the probability of a dependent event is changed by the occurrence of another event. Events A and B are independent if and only if:
P(A|B) = P(A), or equivalently, P(B|A) = P(B)
LOS 9. h: Calculate and interpret an unconditional probability using the total probability rule.
Using the total probability rule, the unconditional probability of A is the probability of weighted sum of the condition probabilities:
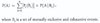
LOS 9. i: Explain the use of conditional expectation in investment applications.
Conditional expected values depend on the outcome of some other event.
Forecasts of expected values for a stock’s return, earnings, and dividends can be refined, using conditional expected values, when new information arrives that affects the expected outcome.
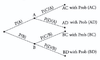
LOS 9. j: Explain the use of a tree diagram to represent an investment problem.
A tree diagram shows the probabilities of two events and the conditional probabilities of two subsequent events.
LOS 9. k: Calculate and interpret covariance and correlation.
Covariance measures the extent to which two random variables tend to be above and below their respective means for each joint realization. It can be calculated as:
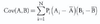
LOS 9. k: Calculate and interpret covariance and correlation.
Correlation is a standardized measure of association between two random variables; it ranges in value form -1 to +1 and is equal to:
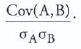
LOS 9. l: Calculate and interpret the expected value, variance, and standard deviation of a random variable and of returns on a portfolio.
The expected value of a random variable, E(X), equals:
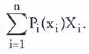
LOS 9. l: Calculate and interpret the expected value, variance, and standard deviation of a random variable and of returns on a portfolio.
The variance of a random variable, Var(X), equals:

LOS 9. l: Calculate and interpret the expected value, variance, and standard deviation of a random variable and of returns on a portfolio.
Standard deviation:
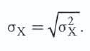
LOS 9. l: Calculate and interpret the expected value, variance, and standard deviation of a random variable and of returns on a portfolio.
The expected returns and variance on a 2-asset portfolio are given by:
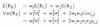
LOS 9. m: Calculate and interpret covariance given a joint probability function.
Given the joint probabilities for Xi and Yi, i.e., P(XiYi), the covariance is calculated as:
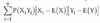
LOS 9. n: Calculate and interpret an updated probability using Bayes’ formula.
Bayes’ formula for updating probabilities based on the occurrence of an event O is:
P(I|O) = [P(O|I) / P(O)] x P(I)
Equivalently, based on the tree diagram below:
P(A|C) = P(AC) / P(AC) + P(BC).

LOS 9. o: Identify the most appropriate method to solve a particular counting problem and solve counting problems using factorial, combination, and permutation concepts.
The number of ways to order n objects in n factorial, n! = n x (n – 1) x (n – 2) x … x 1.
LOS 9. o: Identify the most appropriate method to solve a particular counting problem and solve counting problems using factorial, combination, and permutation concepts. (nCr)
The number of ways to choose a subset of size r from a set of size n (nCr) when order doesn’t matter is: