(11) Hypothesis Testing Flashcards
LOS 12. a: Define a hypothesis, describe the steps of hypothesis testing, and describe and interpret the choice of the null and alternative hypotheses.
Hypothesis: A statement about the value of some effect size or parameter of one or more populations
Hypothesis testing: Evaluating the accuracy of a statement regarding a population parameter or effect size given sample information
LOS 12. a: Define a hypothesis, describe the steps of hypothesis testing, and describe and interpret the choice of the null and alternative hypotheses.
The hypothesis testing process requires:
- State the hypothese (null and an alternative hypothesis)
- Identify the appropriate test statistic and probability distribution
- Specification of the significance level
- State the decision rule
- Collect data and calculate the test/sample statistic
- Make the statistical decision
- Make the real world decision
LOS 12. a: Define a hypothesis, describe the steps of hypothesis testing, and describe and interpret the choice of the null and alternative hypotheses.
The null hypothesis (H0) is what the researcher wants to reject (the statement we are testing). The alternative hypothesis (Ha) is what the researcher wants to support and validate, and it is accepted when the null hypothesis is rejected.
LOS 12. b: Distinguish between one-tailed and two-tailed tests of hypotheses.
A two-tailed test results from a two-sided alternative hypothesis (e.g. Ha: μ ≠ μo).
A one-tailed test results from a one-sided alternative hypothesis (e.g. Ha: μ > μo, or Ha: μ < μo).
LOS 12. c: Explain a test statistic, Type I and Type II errors, a significance level, and how significance levels are used in hypothesis testing.
The test statistic is the value that a decision about a hypothesis will be based on. For a test about the value of the mean of a distribution:
Test statistic = (sample mean – hypothesized mean) / (standard error of sample mean)
Standard error = standard deviation / square root of sample size
LOS 12. c: Explain a test statistic, Type I and Type II errors, a significance level, and how significance levels are used in hypothesis testing.
A Type I error is the rejection of the null hypothesis when it is actually true, while a type II error is the failure to reject the null hypothesis when it is actually false.
Both of these can be reduced by increasing the sample size.
Probability of a type 1 error = alpha
Probability of a type II error = beta
LOS 12. c: Explain a test statistic, Type I and Type II errors, a significance level, and how significance levels are used in hypothesis testing.
The significance level can be interpreted as the probability that a test statistic will reject the null hypothesis by chance when it is actually true (i.e., the probability of a Type I error). A significance level must be specified to select the critical values for the test.
LOS 12. d: Explain a decision rule, the power of a test, and the relation between confidence intervals and hypothesis tests.
Hypothesis testing compares a computed test statistic to a critical value at a stated level of significance, which is the decision rule for the test.
Right tail test: reject the null hypothesis (H0) when the test statistic is greater than the critical value
Left tail test: reject the null when the test statistic is less than the critical value
Two-tailed test: reject the null when the absolute value of the test statistic is greater than the absolute value of the critical value
Critical value is the rejection point
LOS 12. d: Explain a decision rule, the power of a test, and the relation between confidence intervals and hypothesis tests.
The power of a test is the probability of rejecting the null when it is false. The power of a test = 1 – P(Type II error).
If the null hypothesis is rejected, the result is statistically significant
LOS 12. d: Explain a decision rule, the power of a test, and the relation between confidence intervals and hypothesis tests.
A hypothesis about a population parameter is rejected when the sample statistic lies outside a confidence interval around the hypothesized value for the chosen level of significance.
LOS 12. e: Distinguish between a statistical result and an economically meaningful result.
Statistical significance does not necessarily imply economic significance. Even though a test statistic is significant statistically, the size of the gains to a strategy to exploit a statistically significant result may be absolutely small or simply not great enough to outweigh transaction costs, taxes, risk.
LOS 12. f: Explain and interpret the p-value as it relates to hypothesis testing.
The p-value for a hypothesis test is the smallest significance level for which the hypothesis would be rejected. For example, a p-value of 7% means that hypothesis can be rejected at the 10% significance level but cannot be rejected at the 5% significance level.
The smaller the p-value, the stronger the evidence
LOS 12. g: Identify the appropriate test statistic and interpret the results for a hypothesis test concerning the population mean and both large and small samples when the population is normally or approximately normally distributed and the variance is 1) known or 2) unknown.
With unknown population variance, the t-statistic is used for tests about the mean of a normally distributed population.
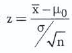
LOS 12. g: Identify the appropriate test statistic and interpret the results for a hypothesis test concerning the population mean and both large and small samples when the population is normally or approximately normally distributed and the variance is 1) known or 2) unknown.
If the population variance is known, the appropriate test statistic is (equation) for test about the mean of a population.
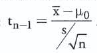
LOS 12. h: Identify the appropriate test statistic and interpret the results for a hypothesis test concerning the equality of the population means of two at least approximately normally distributed populations, based on independent random samples with 1) equal or 2) unequal assumed variances.
For two independent samples from two normally distributed populations, the difference in means can be tested with a t-statistic. When the two population variances are assumed to be equal, the denominator is based on the variance of the pooled samples, but when sample variances are assumed to be unequal, the denominator is based on a combination of the two samples’ variances.
LOS 12. i: Identify the appropriate test statistic and interpret the results for a hypothesis test concerning the mean difference of two normally distributed populations.
LOS 12. j: Identify the appropriate test statistic and interpret the results for a hypothesis test concerning 1) the variance of a normally distributed population, and 2) the equality of the variances of two normally distributed populations based on two independent random samples.
Right tail for critical value of chi square is: alpha divided by 2
Left tail for critical value of chi square is: 1 - (alpha divided by 2)
Must look up both values in chi square
LOS 12. j: Identify the appropriate test statistic and interpret the results for a hypothesis test concerning 1) the variance of a normally distributed population, and 2) the equality of the variances of two normally distributed populations based on two independent random samples.
Comparing two variances
Use the larger variance as the numerator
Critical value used = Falpha/2, n1 - 1, n2 -1
LOS 12. k: Formulate a test of the hypothesis that the population correlation coefficient equals zero and determine whether the hypothesis is rejected at a given level of significance
Testing the strength of a linear relationship between 2 variables (i.e. correlation). This is a two tailed test
