(46) Understanding Fixed-Income Risk and Return Flashcards
LOS 55. a: Calculate and interpret the sources of return from investing in a fixed-rate bond.
Sources of return for a bond investment include:
- Coupon and principal payments (credit risk)
- Reinvestment of coupon payments (interest rate risk)
- Capital gain or loss if bond is sold before maturity (interest rate risk).
Changes in YTM produce market price risk (uncertainty about a bond’s price) and reinvestment risk (uncertainty about the income from reinvesting coupon payments). An increase (a decrease) in YTM decreases (increases) a bond’s price but increases (decreases) its reinvestment income.
LOS 55. b: Define, calculate, and interpret Macaulay, modified, and effective durations.
Macaulay duration is the weighted average number of coupon periods until a bond’s scheduled cash flows.
LOS 55. b: Define, calculate, and interpret Macaulay, modified, and effective durations.
Modified duration is a linear estimate of the percentage change in a bond’s price that would result form a 1% change in its YTM. (When interest rates drop, %change in PV full goes up)
ModDur = MacDur/(1+r)
Always want mod duration to be an annualized amount
% Change in full price of bond(PVfull) = - AnnModDur x change in yield
Change in yield is change in rates
If Macauley duration is unknown, we can approximate Modified duration using the formula below
LOS 55. b: Define, calculate, and interpret Macaulay, modified, and effective durations.
Effective duration is a linear estimate of the percentage change in a bond’s price that would result from a 1% change in the benchmark yield curve. (used for complex bonds with embedded options such as callable bonds)
Requires an option pricing model for (V-)
LOS 55. c: Explain why effective duration is the most appropriate measure of interest rate risk for bonds with embedded options.
Effective duration is the appropriate measure of interest rate risk for bonds with embedded options because changes in interest rates may change their future cash flows. Pricing models are used to determine the prices that would result from a given size change in the benchmark yield curve.
(Modified and macauley duration are useless for bonds with embedded options)
LOS 55. d: Define key rate duration and describe the use of key rate durations in measuring the sensitivity of bonds to changes in the shape of the benchmark yield curve.
Key rate duration is a measure of the price sensitivity of a bond or a bond portfolio to a change in the spot rate for a specific maturity. We can use the key rate durations of a bond or portfolio to estimate its price sensitivity to changes in the shape of the yield curve.
Key rate duration must be be used to estimate % change in portfolio value
You get a different key rate duration for each maturity. The sum of all key rate durations equal the effective duration
LOS 55. e: Explain how a bond’s maturity, coupon, and yield level affect its interest rate risk.
Holding other factors constant:
- Duration increases when maturity increases
- Duration decreases when the coupon rate increases (less interest rate risk)
- Duration decreases when YTM increases.
LOS 55. f: Calculate the duration of a portfolio and explain the limitations of portfolio duration.
There are two methods for calculating portfolio duration:
- Calculate the weighted average number of periods until cash flows will be received using the portfolio’s IRR (its cash flow yield). This method is better theoretically but cannot be used for bonds with options.
- Calculate the weighted average of durations of bonds in the portfolio (the method most often used). Portfolio duration is the percentage change in portfolio value for a 1% change in yield, only for parallel shifts of the yield curve.
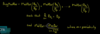
LOS 55. g: Calculate and interpret the money duration of a bond and price value of a basis point (PVBP)
Measure of price change in currency terms
Money duration is stated in currency units and is sometimes expressed per 100 of bond value.
Money duration = annual modified duration x full price of bond position
Money duration per 100 units of par value = annual modified duration x full bond price per 100 of par value
LOS 55. g: Calculate and interpret the money duration of a bond and price value of a basis point (PVBP)
The price value of a basis point is the change in the value of a bond, expressed in currency units, for a change in YTM of one basis point, or 0.01%
PVBP = [(V- - V+)/2]
or
Basis point value (BVP) = money duration x change in yield
LOS 55. h: Calculate and interpret approximate convexity and distinguish between approximate and effective convexity.
Change in PV due to duration - primary effect
Change in PV due to convexity - secondary effect (only for large changes in basis points)
In the formula below V = present value
LOS 55. i: Estimate the percentage price change of a bond for a specified change in yield, given the bond’s approximate duration and convexity.
Given values for approximate annual modified duration and approximate annual convexity, the percentage change in the full price of a bond can be estimated as:
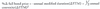
LOS 55. j: Describe how the term structure of yield volatility affects the interest rate risk of a bond.
Yield volatility = # of basis points change
The term structure of yield volatility refers to the relationship between maturity and yield volatility. Short-term yields may be more volatile than long-term yields. As a result, a short-term bond may have more positive volatility than a longer-term bond with a higher duration.
LOS 55. k: Describe the relationships among a bond’s holding period return, its duration, and the investment horizon.
Over a short investment horizon (duration gap > 0), a change in YTM affects market price more than it affects reinvestment income.
Over a long investment horizon (duration gap <0), a change in YTM affects reinvestment income more than it affects market price.
Macaulay duration may be interpreted as the investment horizon for which a bond’s market price risk and reinvestment risk just offset each other.
Duration gap = Macaulay duration – investment horizon.
LOS 55. l: Explain how changes in credit spread and liquidity affect yield-to-maturity of a bond and how duration and convexity can be used to estimate the price effect of the changes.
A bond’s yield spread to the benchmark curve includes a premium for credit risk and a premium for illiquidity.
Given values for duration and convexity, the effect on the value of a bond from a given change in its yield spread (Δspread) can be estimated as:
-duration(Δspread) + ½ convexity (Δspread)2
