333) ST5: Mean, Variance and Standard Deviation.

Question 1

What does Greek symbol (mu) stands for?

Answer 1

It stands for exact population mean, when we have all measurements.

Question 2

How are we finding Calculated Population Variance?

Why are we squaring each (x-(mu))?

Answer 2

Using expression:

Population Variance = Sum of squared subtraction of the population mean (mu) from each measurement, x and divided by the number of measurements.

To get positive values.

Question 3

How we are getting Population Standard Deviation?

Answer 3

The square root of population Variance.

The square root of sum of measurment minus population mean squared and divided by the number of measurments.

Question 4

Formula of Estimated Population Variance?

Answer 4

Sum of measurment minus mean squared and divided by number of measurements minus 1.

Question 5

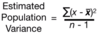
Estimated Population Standard Deviation (s)?

Answer 5

Square root of sum of squared deviations divided by numbre of measurements minus 1.

Question 6

Properties of the Standard Deviation?

Answer 6

1. s > 0.
2. s= 0 only when all observations have the same value.
3. The greater the variability about the mean, the larger is the value of s.

Question 7

Empirical Rule.

Answer 7

If the histogram of the data is approximately bell shaped, then:

1. About 68% of the observations fall between y-bar - s and y-bar + s.
2. About 95% of the observations fall between y-bar - 2s and y-bar + 2s.
3. All or nearly all observations fall between y - 3s and y + 3s.