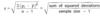222) 3) Chapter 3: Descriptive Statistics

Question 1

What two key features quantitative variables describe numerically according to descriptive statistics?

Answer 1

The center of the data: typical observation. The variability of the data: the spread around the center.

Question 2

Comparing qualitative categories using relative frequencies?

Answer 2

Relative frequency is the proportion or percentage of the observations that fall in that category.

Question 3

Histograms?

Answer 3

A graph of a relative frequency distribution for a quantitative variable is called a histogram.

Question 4

The Mean?

Answer 4

AVERAGE. The best known and most commonly used measure of the center is the mean. Mean is the sum of the observations divided by the number of observations.

Question 5

What denotes this symbol?

Answer 5

Sample Size.

Question 6

What is denoted by this symbol?

Answer 6

The variable.

Question 7

What is denoted by this symbols? y1 y2 ….

Answer 7

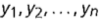
Observations.

The n sample observations on a variable y are denoted by y1 for the first observation, y2 for the second and so forth.

Question 8

What is denoted by this symbol?

Answer 8

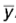
Read as y-bar.

Denotes sample mean.

Question 9

What says the definition of sample mean?

Sample mean is y-bar.

Answer 9

It says that:

Question 10

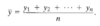
Shortened expression for the samle mean of n observations?

Answer 10

Sample mean is equal to sum of all variables divided by number of observations.

Question 11

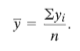
What is outlier for the mean?

Answer 11

When one observation is much larger or smaller that the others, such as in highly skewed distrbutions.

Question 12

Properties of the mean?

Answer 12

1. Formula for the mean uses numerical values for the observations so it is appropriate only for quantitative variables.
2. The mean can be higly influenced by an observation that falls well above or well below the bulk of the data, called an outlier.

Question 13

What is weighted average for combined set of observations (2 sets of data with sample sizes n1;n2)

Answer 13

Expressed by sample mean multiplied by sample size of first data set + sample mean multiplied by sample size of second data set divided by sum of sample sizes of both data sets.

Question 14

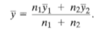
What is median?

Answer 14

The median is the observations that falls in the middle of the ordered sample. When the sample size n is odd, a single observation occurs in the middle. When the sample size is even two middle observations occur, and the median is the midpoint between two.

Index of middle observation?

Question 15

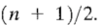
Properties of the median?

Answer 15

1. Median like a mean is appropriate for quantitative variables.

Also valid for ordinal-scale (requires oredered observations).

Not appropriate for nominal-scale data.

2. For symmetric distributions median and the mean are identical
3. For skewed distributions mean lies toward the direction of skew (longer tail) relative to the median.
4. The median is insensitive to the distance of the observations (variable values).
5. Is not affected by outliers.

Question 16

In which cases mean or median are mostly preferred?

Answer 16

If a distribution is higly skewed the median is usually preferred because it better represents what is typical

If the distribution is close to symmetric or only mildly skewed or of it is discrete with few distinct values, the mean is usually prefferred, because it uses the numerical values of all observations.

Question 17

What is Mode?

Answer 17

The mode is value that occurs most frequently.

Question 18

Properties of mode?

Answer 18

1. Apporpriate for all types of data.
2. Can get bimodal value. If answers are polarized there ir 2 almost equal often answers.
3. Mean, median, and mode are identical for unimodal, symmetric distribution.

Question 19

Variability of the data?

What is range?

Answer 19

When the relative frequency for one observation is higher that same relative frequency for another observation.

Range is difference between the largest and smallest observation.

Question 20

Describe range?

Answer 20

When one observations has more and greater variability than another observation.

Question 21

Deviation from the sample mean y-bar?

Answer 21

Deviation of an observation yi from the sample mean y-bar is: image 1

Question 22

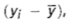
When the deviation is negative or positive?

Answer 22

If the observation falls below the mean deviation is negative.

Question 23

Standard deviation expression?

Answer 23