Wk 12: Modelling Association Flashcards
(24 cards)
If we carry out 1 hypothesis test with a significance threshold of 5%, the probability of making a type 1 error is ____ %.
5
If we carry out 10 hypothesis tests with a significance threshold of 5%, the probability of making a type 1 error is ____ %. Why?
>5
- If you are doing multiple comparisons, in order to reduce the chance of type 1 error, we decrease the significance level to 5%/10 (Bonferroni correction), so overall significant level is <5%. Or we look at Tukey HSD.

If we carry out 1 hypothesis test with a significance threshold of 5%, the probability of making a type 2 error depends on _____. Why?
(1 - power)
- To increase power, we can increase sample size, increase effect size, decrease errors, decrease methodological variability.
- Experiment with >80% power is worthwhile.
- Power analysis needs survey of literature, small sample study (pilot study), in order to figure out a clinically relevant sample size, typical variability etc. before the real experiment.
What are 4 characteristics?
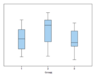
- All are normal distribution, but because of small sample (n = 20), they look skewed.
- 1st box plot: Normal.
- 2nd box plot: Median is far from the centre. Whiskers are negatively skewed.
- 3rd box plot: Median is positively skewed. Whiskers are negatively skewed.
What are 3 characteristics?
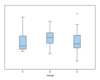
- 1st box plot: Not normal. Positively skewed.
- 2nd box plot: Normal.
- 3rd box plot: Chance of seeing 1 outlier in normal distribution is 1% - acceptable.
What are 4 characteristics?

- n = 100
- 1st box plot: 3-4 outliers in a sample >20 is not normal - seriously deviated.
- 2nd box plot: 1 outlier is acceptable. Normal.
- 3rd box plot: Normal.
What is a simple linear regression?
- The mean response is given by a straight line with constant normal variability about that line.
- Least-squares line: A line that minimises the sum of the squared residuals.
What are 4 assumptions for linear regressions?
- Independent observations
- Linear association
- Normal variability
- Skews do not matter as much for large sample size because it will approach normally distribution (central limit theorem).
- But skews will undermine predictions made by the linear model. You can log transform the data to get rid of the skew.
- Can again check normal variability by checking residuals on scatter plot, P-P plot & histogram.
- Equal variances
What are regression models that use a straight line to estimate the mean response based on a predictor? What are 4 characteristics?
y = b0 + b1x
- y is the mean response
- x is the predictor
- Null hypothesis: The slope in the relationship is 0 (flat line).
-
P-value is the probability of getting the b1 value by chance if there was no relationship between the response and the predictor.
- p < 0.05 suggests there is evidence against the null hypothesis, so there is a relationship between the response and the pred ictor.
What are 3 characteristics?

- Null hypothesis: height does not affect mass (flat line).
- Mass and height show positive association (line going up).
- Residual is the vertical distance from each dot to the line.
- Dots above line have positive residual ○ Dots below line have negative residual
What are 2 characteristics?

Checking residuals on scatter plot (simple linear regression)
- A constant band of dots suggests normal variability. Dots not converging or diverging.
- In this, the left side has less variability, the right side has more variability.
What are 3 characteristics?

Checking residuals on P-P plot (simple linear regression)
- If you have normal distribution, the dots should fall on the line.
- This shows deviations in the middle, so the residuals are not normal
- Deviations on top or bottom do not matter as much as middle
What are 2 characteristics?

Checking residuals on histogram (simple linear regression)
- Normal distribution should be a bell curve
- Positively skewed distribution
What are 2 characteristics?

Interpretations of Tukey HSD
- p = 0.674 means there is no difference between “last” and “uncertain”
- p < 0.001 means there is a significant difference between the other groups.
What are 3 characteristics?

Interpretation of linear regression tables
Model summary table
- R is the Pearson correlation coefficient.
- R square is the % of variability explained by the model.
- For simple linear regression, R square is the square of Pearson correlation coefficient ®.
- R square (0.556) means the linear regression model explains 55.6% of the variability.
What are 6 characteristics?

- p < 0.001 mean there is an association between the variables.
- “Total” row corresponds to the sample standard deviation.
- Amount of groups is df + 1
- Amount of participants is 396 + 1 = 397 297
- Residual df is n - 2 since we need to estimate an intercept and slope before we can estimate residual variability.
- Regression df is 1 because we have 1 variable.
What are 2 characteristics?

Coefficients table
- Standard error measures how uncertain we are about the parameter estimate.
- t = B / Std. Error. T value suggests that hearing B (0.126) is 12.37 standard errors away from the mean, which is unlikely (p < 0.001).
What is a multiple linear regression? What is the dummy/indicator variable? What is the H0?

- Regression allows us to model the effects of multiple variables on a response.
- y = b0 + b1x1 + b2x2
- A dummy/indicator variable (x) codes a nominal variable as 1 and 0, so you can put it in linear regression.
- Null hypothesis: There is no difference between the groups.
What is a characteristic?

Checking residuals on histogram (multiple linear regression)
- Roughly normal distribution
What are 2 characteristics?

Checking residuals on P-P plot (multiple linear regression)
- Roughly normal
- In the middle, the big jump on both sides is a bit weird
What is a characteristic?

Checking residuals on scatter plot (multiple linear regression)
- Constant band of dots suggests normal variability
What are 2 interpretations of multiple linear regression?

Interpretation of multiple linear regression
- P < 0.001 suggests there is significant evidence of a hearing effect, after taking into account the age group; and significant evidence of an age effect, after taking into account the hearing level.
- In simple linear regression, hearing B was 0.126. Now taking in account of age, the hearing B is 0.088, meaning that some of the original relationship was actually due to the different age.
What are 2 characteristics?

- p = 0.001 means there is an association between working memory & QuickSIN score.
- TestA B score -0.046 means negative association
What are 3 characteristics?

- Age has insignificant association with QuickSIN score (p = 0.605)
- Hearing has significant association with QuickSIN score (p < 0.001)
- Working memory has weak significant association with QuickSIN score (p < 0.094)


